题目内容
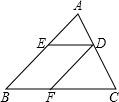 如图,DE∥BC,DF∥AB,△ADE的面积为4,△CDF的面积为9,四边形BFDE的面积为________.
如图,DE∥BC,DF∥AB,△ADE的面积为4,△CDF的面积为9,四边形BFDE的面积为________.
12
分析:由DE∥BC,DF∥AB可推出△ADE∽△ACB、△CDF∽△CAB,然后利用相似三角形面积之比等于相似比的平方可得 =
=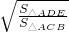 ,
, =
=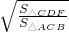 ,又因为
,又因为 +
+ =1,从而建立方程,解出四边形BFDE的面积.
=1,从而建立方程,解出四边形BFDE的面积.
解答:∵DE∥BC,∴△ADE∽△ACB
∴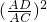 =
= ,即
,即 =
=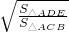 ,
,
同理,由DF∥AB可得 =
=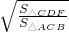 ,
,
∵ +
+ =1,△ADE的面积为4,△CDF的面积为9,
=1,△ADE的面积为4,△CDF的面积为9,
∴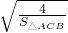
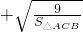 =1,
=1,
解得S△ACB=25,
故四边形BFDE的面积为25-9-4=12.
点评:此题主要考查平行线分线段成比例定理和相似三角形面积之比等于相似比的平方的理解及运用.
分析:由DE∥BC,DF∥AB可推出△ADE∽△ACB、△CDF∽△CAB,然后利用相似三角形面积之比等于相似比的平方可得
 =
=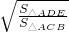 ,
, =
=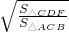 ,又因为
,又因为 +
+ =1,从而建立方程,解出四边形BFDE的面积.
=1,从而建立方程,解出四边形BFDE的面积.解答:∵DE∥BC,∴△ADE∽△ACB
∴
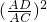 =
= ,即
,即 =
=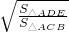 ,
,同理,由DF∥AB可得
 =
=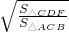 ,
,∵
 +
+ =1,△ADE的面积为4,△CDF的面积为9,
=1,△ADE的面积为4,△CDF的面积为9,∴
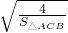
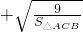 =1,
=1,解得S△ACB=25,
故四边形BFDE的面积为25-9-4=12.
点评:此题主要考查平行线分线段成比例定理和相似三角形面积之比等于相似比的平方的理解及运用.

练习册系列答案
相关题目
 如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE的长为
如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE的长为 12、如图,DE∥BC,将△ABC沿DE所在的直线折叠,点A正好落在BC边上F处,若∠B=40°,则∠BDF=
12、如图,DE∥BC,将△ABC沿DE所在的直线折叠,点A正好落在BC边上F处,若∠B=40°,则∠BDF= 如图,DE∥BC,AD:DB=3:4,则△ADE与△ABC的周长之比为
如图,DE∥BC,AD:DB=3:4,则△ADE与△ABC的周长之比为 (1997•广西)如图,DE∥BC,AB=15,AC=9,BD=4,那么AE=( )
(1997•广西)如图,DE∥BC,AB=15,AC=9,BD=4,那么AE=( ) (1997•河北)已知:如图,DE∥BC,AD=3.6,DB=2.4,AC=7.求EC的长.
(1997•河北)已知:如图,DE∥BC,AD=3.6,DB=2.4,AC=7.求EC的长.