题目内容
10.若方程组$\left\{\begin{array}{l}ax+by=4\\ bx+ay=5\end{array}\right.$的解是$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$,则a+b的值为( )| A. | 3 | B. | -3 | C. | -2 | D. | 2 |
分析 把$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$代入方程组$\left\{\begin{array}{l}ax+by=4\\ bx+ay=5\end{array}\right.$可得$\left\{\begin{array}{l}{2a+b=4①}\\{2b+a=5②}\end{array}\right.$,再利用①+②可得答案.
解答 解:把$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$代入方程组$\left\{\begin{array}{l}ax+by=4\\ bx+ay=5\end{array}\right.$得:$\left\{\begin{array}{l}{2a+b=4①}\\{2b+a=5②}\end{array}\right.$,
①+②得:3a+3b=9,
a+b=3,
故选:A.
点评 此题主要考查了二元一次方程组的解,当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.若$\sqrt{a}$和$\sqrt{-a}$都有意义,则a应满足的条件是( )
| A. | a≥0 | B. | a≤0 | C. | a=0 | D. | a≠0 |
5.观察下列4个命题:其中真命题是( )
(1)直线a、b、c,如果a⊥b、b⊥c,那么a⊥c;(2)三角形的三个内角中至少有两个锐角;(3)平移变换中,各组对应点连成两线段平行且相等;(4)三角形的外角和是180°.
(1)直线a、b、c,如果a⊥b、b⊥c,那么a⊥c;(2)三角形的三个内角中至少有两个锐角;(3)平移变换中,各组对应点连成两线段平行且相等;(4)三角形的外角和是180°.
| A. | (1)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
2.下列实数中,无理数是( )
| A. | $\frac{1}{3}$ | B. | $\sqrt{16}$ | C. | $\sqrt{7}$ | D. | $\root{3}{-27}$ |
19.直线y=-$\frac{1}{6}$x+2经过的象限是( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
20.如图图案不是轴对称图形的有( )个. 

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
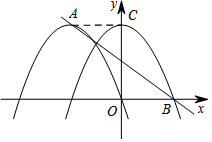 如图,抛物线y1=-$\frac{3}{4}$x2-3x的顶点为A,直线y=ax+b经过点A,交x轴的正半轴于点B,将抛物线y1=-$\frac{3}{4}$x2-3x向右平移,顶点落在y轴上的点C时,得到抛物线y2刚好经过点B.
如图,抛物线y1=-$\frac{3}{4}$x2-3x的顶点为A,直线y=ax+b经过点A,交x轴的正半轴于点B,将抛物线y1=-$\frac{3}{4}$x2-3x向右平移,顶点落在y轴上的点C时,得到抛物线y2刚好经过点B.