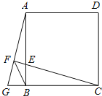
题目内容
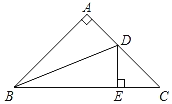
【题目】如图,已知![]() ,以
,以![]() 为直径,
为直径,![]() 为圆心的半圆交
为圆心的半圆交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的角平分线,且
的角平分线,且![]() ,垂足为点
,垂足为点![]() .
.
![]() 判断直线
判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】![]() 直线
直线![]() 与
与![]() 的位置关系是相切,理由见解析;
的位置关系是相切,理由见解析;![]()
![]() .
.
【解析】
(1)连接CE,推出AD∥CE,得出∠ECM=∠DAC=∠DAB=∠EBC,根据∠AHB=90°推出∠DAB+∠ABE=90°.代入推出∠ABE+∠EBC=90°,根据切线的判定推出即可;
(2)求出AC长,求出AM=AB=3,求出CM=2,证△ECM∽△EBC,得出比例式,推出BE=2EC,在△BEC中,根据勾股定理即可求出BE.
![]() 直线
直线![]() 与
与![]() 的位置关系是相切,
的位置关系是相切,
理由是:连接![]() ,
,
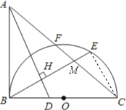
∵![]() 为直径,
为直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵弧![]() 弧
弧![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
又∵![]() 经过直径的外端,
经过直径的外端,
∴![]() 是圆
是圆![]() 的切线.
的切线.
![]() ∵
∵![]() ,
,![]() .由
.由![]() 知,
知,![]() 是直角三角形,由勾股定理得:
是直角三角形,由勾股定理得:![]() .
.
在![]() 中,
中,![]() 于
于![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目