Question

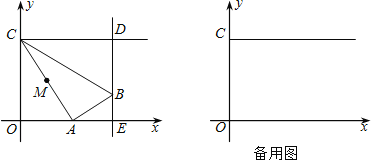
【题目】如图，在正方形ABCD中，E是BC边上的一点，BE=4，EC=8，将正方形边AB延AE折叠刀AF，延长EF交DC于G，连接AG，现在有如下结论：①∠EAG=45°；②GC=CF；③FC∥AG；④S△GFC=14.4；其中结论正确的个数是（ ）

A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

选项①正确．证明∠GAF=∠GAD，∠EAB=∠EAF即可．选项②错误．可以证明DG=GC=FG，显然△GFC不是等边三角形，可得结论．选项③正确．证明CF⊥DF，AG⊥DF即可．选项④正确．证明FG：EG=3：5，求出△ECG的面积即可．

解：如图，连接DF．

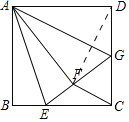
∵四边形ABCD是正方形，

∴AB=AD=BC=CD，∠ABE=∠BAD=∠ADG=∠ECG=90°，

由折叠可知：AB=AF，∠ABE=∠AFE=∠AFG=90°，BE=EF=4，∠BAE=∠EAF，

∵∠AFG=∠ADG=90°，AG=AG，AD=AF，

∴Rt△AGD≌Rt△AGF（HL），

∴∠GAF=∠GAD，

∴∠EAG=∠EAF+∠GAF=(∠BAF+∠DAF)=45°，故①正确，

设GD=GF=x，

在Rt△ECG中，∵EG2=EC2+CG2，

∴(4+x)2=82+(12-x)2，

∴x=6，

∵CD=BC=BE+EC=12，

∴DG=CG=6，

∴FG=GC，

易知△GFC不是等边三角形，显然FG≠FC，故②错误，

∵GF=GD=GC，

∴∠DFC=90°，

∴CF⊥DF，

∵AD=AF，GD=GF，

∴AG⊥DF，

∴CF∥AG，故③正确，

∵S△ECG=×6×8=24，FG：FE=6：4=3：2，

∴FG：EG=3：5，

∴S△GFC=×24==14.4，故④正确，

故①③④正确，

故选：C．