Question

19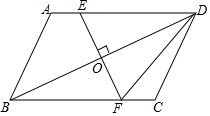．已知：如图，AD∥BC，EF垂直平分BD，与AD，BC，BD分别交于点E，F，O．求证：
（1）△BOF≌△DOE；
（2）DE=DF．

Answer 1

分析 （1）由线段垂直平分线的定义可知OB=OD，且∠BOF=∠EOD，利用平行可得∠BFO=∠DEO，利用AAS可证明△BOF≌△DOE；
（2）由（1）中的全等可得OE=OF，可知BD是EF的垂直平分线，可得DE=DF．

解答 证明：
（1）∵AD∥BC，
∴∠BFO=∠DEO，
∵EF垂直平分BD，
∴OB=OD，∠BOF=∠DOE=90°，
在△BOF和△DOE中
$\left\{\begin{array}{l}{∠BOF=∠DOE}\\{∠BFO=∠DEO}\\{OB=OD}\end{array}\right.$
∴△BOF≌△DOE（AAS）；
（2）由（1）可知△BOF≌△DOE，
∴OE=OF，且BD⊥EF，
∴BD为线段EF的垂直平分线，
∴DE=DF．

点评 本题主要考查全等三角形的判定和性质及线段垂直平分线的性质，利用条件证明△BOF≌△DOE是解题的关键．