题目内容
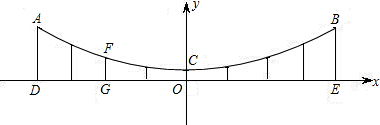
某桥的部分横截面如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为x轴,经过抛物线的顶点C与x轴垂直的直线为y轴,建立平面直角坐标系.已知此桥垂直于桥面的相邻两柱之间距离为2m(图中用线段AD、CO、BE等表示桥柱),CO=1m,FG=2m
(1)求经过A、B、C三点的抛物线相应的二次函数关系式;
(2)求柱子AD的高度.
(1)求经过A、B、C三点的抛物线相应的二次函数关系式;
(2)求柱子AD的高度.

考点:二次函数的应用
专题:
分析:(1)设抛物线的解析式为y=ax2+cc,就有F(-4,2),C(0,1),由待定系数法就可以求出结论;
(2)相邻两柱之间距离为2m就可以得出OD=8,就有D的横坐标为-8,将D的横坐标为-8代入解析式就可以求出AD的值.
(2)相邻两柱之间距离为2m就可以得出OD=8,就有D的横坐标为-8,将D的横坐标为-8代入解析式就可以求出AD的值.
解答:解:(1)∵CO=1m,
∴C(0,1).
∵垂直于桥面的相邻两柱之间距离为2m,
∴OG=4.
∵FG=2m,
∴F(-4,2).
设抛物线的解析式为y=ax2+c,由题意,得
,
解得:
,
∴二次函数的关系式为:y=
x2+1;
(2)∵相邻两柱之间距离为2m,
∴OD=8.
∴D的横坐标为-8,
∴y=
×64+1=5m.
答:AD的高度为5m.
∴C(0,1).
∵垂直于桥面的相邻两柱之间距离为2m,
∴OG=4.
∵FG=2m,
∴F(-4,2).
设抛物线的解析式为y=ax2+c,由题意,得
|
解得:
|
∴二次函数的关系式为:y=
| 1 |
| 16 |
(2)∵相邻两柱之间距离为2m,
∴OD=8.
∴D的横坐标为-8,
∴y=
| 1 |
| 16 |
答:AD的高度为5m.
点评:本题考查了运用待定系数法求二次函数的解析式的运用,由函数的解析式根据自变量的值求函数值的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
 如图所示,在四边形ABCD中,∠A=∠C=90°,BE、DF分别平分∠ABC、∠ADC.判断BE、DF是否平行,并说明理由.
如图所示,在四边形ABCD中,∠A=∠C=90°,BE、DF分别平分∠ABC、∠ADC.判断BE、DF是否平行,并说明理由. 图中有
图中有