题目内容
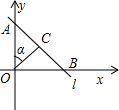如图，直线l交两坐标轴于A、B，点C在线段AB上，若∠AOC=a，OA=OB，那么S△OBC：S△OAC=
- A.sinα
- B.cosα
- C.tanα
- D.cotα
D
分析：作CD⊥y轴于点D，CE⊥x轴于点E．根据两三角形中AO=BO，得出S△OBC：S△OAC=CE：CD；
再根据三角函数化简即可得出CE和CD的比值．
解答：
解：作CD⊥y轴于点D，CE⊥x轴于点E．
∵OA=OB，
∴S△OBC：S△OAC=CE：CD=OC•sin（
-α）：OC•sinα=cosα：sinα=cotα．
故选D．
点评：本题用到的知识点为：等底的两个三角形，面积之比就等于高的比．
分析：作CD⊥y轴于点D，CE⊥x轴于点E．根据两三角形中AO=BO，得出S△OBC：S△OAC=CE：CD；
再根据三角函数化简即可得出CE和CD的比值．
解答：
解：作CD⊥y轴于点D，CE⊥x轴于点E．∵OA=OB，
∴S△OBC：S△OAC=CE：CD=OC•sin（
-α）：OC•sinα=cosα：sinα=cotα．故选D．
点评：本题用到的知识点为：等底的两个三角形，面积之比就等于高的比．
练习册系列答案
相关题目
第一象内的点过点P作PM⊥x轴于M、PN⊥y轴于N．两垂线与直线AB交于E、F．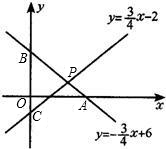
如图，直线y=-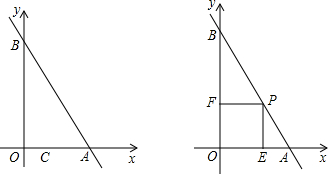
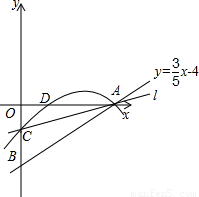
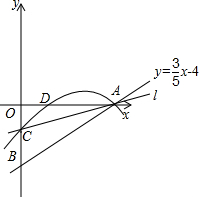如图，直线y=
x-4分别交x、y轴于A、B两点，O为坐标原点．
x-4分别交x、y轴于A、B两点，O为坐标原点．