题目内容
反比例函数y=-
（k为常数，k≠0）的图象位于（ ）
| k2+2k+3 |
| x |
| A、第一、二象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |
分析：先用配方法判断出k2+2k+3＞0，再判断出-（k2+2k+3）＜0，根据反比例函数的性质，即可求出
反比例函数图象所在象限．
反比例函数图象所在象限．
解答：解：∵k2+2k+3=（k+1）2+2＞0，
∴-（k2+2k+3）＜0，
y=-
即：y=
，
根据反比例函数的图象的性质可得，函数的图象在二、四象限，
故选C．
∴-（k2+2k+3）＜0，
y=-
| k2+2k+3 |
| x |
即：y=
| -(k2+2k+3) |
| x |
根据反比例函数的图象的性质可得，函数的图象在二、四象限，
故选C．
点评：利用配方法判断出k2+2k+3的符号是解题的关键．
练习册系列答案
相关题目
如果反比例函数y=-
的图象经过点（x1，y1）（x2，y2），且x1＞x2＞0，那么y1与y2的大小关系是（ ）
| k2+1 |
| x |
| A、y1＜y2 |
| B、y1=y2 |
| C、y1＞y2 |
| D、无法确定 |
如图，矩形ABCD的对角线BD的中点经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=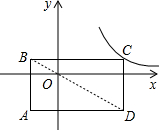
（2012•朝阳）如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=