题目内容
已知⊙O为△ABC的外接圆,圆心O在AB上.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.①求证:OD⊥BC;②求EF的长.

解:(1)尺规作图如图1所示:
(2)①如 图2,∵AD平分∠BAC,
图2,∵AD平分∠BAC,
∴∠DAC=∠BAD,
∵OA=OD,
∴∠OAD=∠D,
∴∠CAD=∠D,
∴AC∥OD,
∴∠ACB=∠OFB,
∵AB是直径,
∴∠ACB=90°,
∴∠OFB=90°,
∴OD⊥BC;
②∵AC∥OD,
∴ =
= ,即
,即 =
= ,
,
∴OF=2,
∵FD=5﹣2=3,
在RT△OFB中,BF= =
= ,
,
∵OD⊥BC,
∴CF=BF= ,
,
∵AC∥OD,
∴△EFD∽△ECA,
∴ =
= =
= ,
,
∴ =
= ,
,
∴EF= CF=
CF= ×
× =
= .
.



练习册系列答案
相关题目



 ,并求其整数解.
,并求其整数解. ,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是( )
,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是( )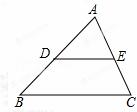
 0° D.70°
0° D.70°
 D.
D.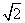
 .
.