题目内容
如图,直线y1=-| 1 |
| 2 |
| 3 |
| 2 |
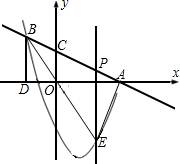 的交点是B,BD⊥x轴,垂足为D,且△ABD的面积是9.
的交点是B,BD⊥x轴,垂足为D,且△ABD的面积是9.(1)求点B的坐标及抛物线的解析式;
(2)抛物线与直线y1的另一个交点为Q,P是线段QB上的一个动点,过P点作y轴的平行线交抛物线于E点,若P的坐标是(m,n),请用关于m的代数式表示线段PE长度;
(3)连接线段BE,QE,是否存在P点,使△QBE的面积S最大?若存在,请求出P点的坐标;若不存在,请说明理由.
分析:(1)先根据直线解析式求出点A的坐标,再设点B的横坐标为x,根据直线解析式表示出纵坐标,然后再根据△ABD的面积是9列出方程即可求出x的值,然后得到点B的坐标,把点B的坐标代入抛物线解析式求出a的值,从而得到抛物线的解析式;
(2)联立直线的解析式与抛物线的解析式求出点Q的坐标,发现点A与点Q重合,再分别求出横坐标为m时的点P与点E的纵坐标的长度,根据两点间的距离即可表示出线段PE的长度;
(3)根据S△QBE=S△PBE+S△PEQ,两三角形都以PE为底边,根据三角形面积公式列式并整理,然后再根据二次函数的最值问题进行求解.
(2)联立直线的解析式与抛物线的解析式求出点Q的坐标,发现点A与点Q重合,再分别求出横坐标为m时的点P与点E的纵坐标的长度,根据两点间的距离即可表示出线段PE的长度;
(3)根据S△QBE=S△PBE+S△PEQ,两三角形都以PE为底边,根据三角形面积公式列式并整理,然后再根据二次函数的最值问题进行求解.
解答:解:(1)当y=0时,-
x+2=0,
解得x=4,
∴点A的坐标是(4,0),
设点B的横坐标是x,则纵坐标为-
x+2,
∴S△ABD=
(4-x)×(-
x+2)=9,
整理得,(x-4)2=36,
解得x=-2或x=10(舍去),
-
x+2=-
×(-2)+2=3,
∴点B的坐标是(-2,3),
∵直线与抛物线y2=ax2-
x-2在第二象限内的交点是B,
∴4a-
×(-2)-2=3,
解得a=
,
∴抛物线的解析式是y=
x2-
x-2;
故答案为:B(-2,3);抛物线的解析式是y=
x2-
x-2;
(2)直线与抛物线解析式联立得,
,
解得
,
,
∴点Q坐标是(4,0),
∵点A坐标也是(4,0),
∴点Q与点A重合,
∵P是线段QB上的一个动点,P的坐标是(m,n),
∴n=-
m+2,
点E的纵坐标是
m2-
m-2,
∴PE=(-
m+2)-(
m2-
m-2)=-
m2+m+4;
(3)假设存在点P(m,n),
则S△QBE=S△PBE+S△PEQ,
=
×(-
m2+m+4)×[m-(-2)]+
×(-
m2+m+4)×(4-m),
=
×(-
m2+m+4)×(m+2+4-m),
=-
(m2-2m-8),
=-
(m-1)2+
,
∵-
<0,
∴存在点P,使△QBE的面积S最大,
当点P的横坐标m=1时,△QBE的面积S最大值是
,
此时n=-
×1+2=
,
∴点P的坐标是(1,
).
| 1 |
| 2 |
解得x=4,
∴点A的坐标是(4,0),
设点B的横坐标是x,则纵坐标为-
| 1 |
| 2 |
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
整理得,(x-4)2=36,
解得x=-2或x=10(舍去),
-
| 1 |
| 2 |
| 1 |
| 2 |
∴点B的坐标是(-2,3),
∵直线与抛物线y2=ax2-
| 3 |
| 2 |
∴4a-
| 3 |
| 2 |
解得a=
| 1 |
| 2 |
∴抛物线的解析式是y=
| 1 |
| 2 |
| 3 |
| 2 |
故答案为:B(-2,3);抛物线的解析式是y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)直线与抛物线解析式联立得,
|

解得
|
|
∴点Q坐标是(4,0),
∵点A坐标也是(4,0),
∴点Q与点A重合,
∵P是线段QB上的一个动点,P的坐标是(m,n),
∴n=-
| 1 |
| 2 |
点E的纵坐标是
| 1 |
| 2 |
| 3 |
| 2 |
∴PE=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
(3)假设存在点P(m,n),
则S△QBE=S△PBE+S△PEQ,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 27 |
| 2 |
∵-
| 3 |
| 2 |
∴存在点P,使△QBE的面积S最大,
当点P的横坐标m=1时,△QBE的面积S最大值是
| 27 |
| 2 |
此时n=-
| 1 |
| 2 |
| 3 |
| 2 |
∴点P的坐标是(1,
| 3 |
| 2 |
点评:本题是二次函数的综合题型,其中涉及的知识点有三角形面积的求解方法,待定系数法求函数解析式,两点的距离公式,解一元二次方程,综合性较强,难度较大,设计本题的巧妙指出在于点A与点Q正好重合,是道不错的好题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
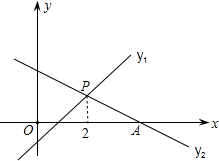 如图,直线y1=
如图,直线y1=| 1 |
| 3 |
| 1 |
| 3 |
| A、x<2 | B、x>2 |
| C、x≤2 | D、x≥2 |
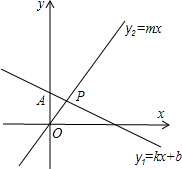 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是
如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是 9、如图,直线y1=k1x+a与y2=k3x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( )
9、如图,直线y1=k1x+a与y2=k3x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( ) 如图:直线y1=-2x+3和直线y2=mx-1分别交y轴于点A、B,两直线交于点C(1,n).
如图:直线y1=-2x+3和直线y2=mx-1分别交y轴于点A、B,两直线交于点C(1,n).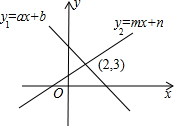 如图,直线y1=ax+b与直线y2=mx+n相交于点(2,3),则不等式ax+b>mx+n的解是( )
如图,直线y1=ax+b与直线y2=mx+n相交于点(2,3),则不等式ax+b>mx+n的解是( )