Question

【题目】如图，二次函数的图象与、轴交于、、三点，其中，抛物线的顶点为．

（1）求的值及顶点的坐标；

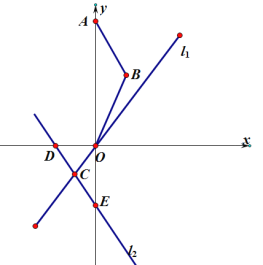
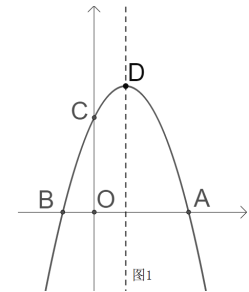
（2）如图1，若动点在第一象限内的抛物线上，动点在对称轴上，当，且时，求此时点的坐标；

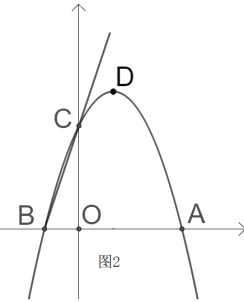
（3）如图2，若点是二次函数图像上对称轴右侧一点，设点到直线的距离为，到抛物线的对称轴的距离为，当时，请求出点的坐标．

Answer 1

【答案】（1），；（2）；（3）．

【解析】

（1）先将把A（3，0）代入，解出m的值，从而得出解析式，再将解析式变为顶点式即可得出D的坐标；

（2）过P点作PM⊥x轴，根据条件证明，即可求出P的坐标；

（3）作对称轴于点，QF平行y轴交延长线于点，于点，设，用含x的表达式，表示出QG和QE，再根据题意列方程，解出x即可．

（1）把A（3，0）代入，

得，

解得：，

∴二次函数的解析式为，

将解析式变为顶点式的形式：，

∴顶点D的坐标为（1，4）；

（2）如图：过P点作PM⊥x轴，

∵点P在上，

∴P（x，-x2+2x+3），

∵，且，

∴∠APM+∠MAP=∠OAN+∠MAP=90°，

∴，

又∵点A的坐标为（3，0），点D坐标为（1，4），

∴，即，

∴，

解得或（舍去），

∴点P的坐标为（1+，2）；

（3）如图：作对称轴于点，QF平行y轴交延长线于点，于点，

∵抛物线解析式为：，

∴可得B（-1，0），C（0，3），

设，，则

∴，

∵QF∥y轴，QG⊥BC，

∴，

∴，

，

或（舍去）

∴．