题目内容
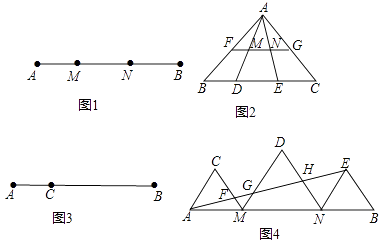
【题目】在Rt△ABC中,∠ACB=90°,点D在边AC上,DE⊥B于点E,连CE.
(1)如图1,已知AC=BC,AD=2CD,
①△ADE与△ABC面积之比;
②求tan∠ECB的值;
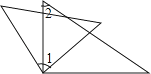
(2)如图2,已知 ![]() =
= ![]() =k,求tan∠ECB的值(用含k的代数式表示).
=k,求tan∠ECB的值(用含k的代数式表示).
【答案】
(1)
解:①作EH⊥AD于H,如图1,设CD=x,则AD=2x,AC=BC=3x,
∵AC=BC,∠ACB=90°,
∴△ACB为等腰直角三角形,
∴∠A=45°,
而DE⊥AB,
∴△ADE为等腰直角三角形,
∴AH=HDF=HE=x,
∴S△ADE= ![]() 2xx=x2,
2xx=x2,
∵S△ACB= ![]() 3x3x=
3x3x= ![]() x2,
x2,
∴ ![]() =
= ![]() =
= ![]() ;
;
②在Rt△CHE中,tan∠HEC= ![]() =
= ![]() =2,
=2,
∵HE∥BC,
∴∠BCE=∠HEC,
∴tan∠ECB=2;
(2)
解:作EH⊥AD于H,如图2,设CD=a,

∵ ![]() =
= ![]() =k,
=k,
∴AD=ak,BC=kAC,
∴AC=(k+1)a,
∴BC=(k2+k)a,
∴AB= ![]() =(k+1)
=(k+1) ![]() a,
a,
∵DE⊥AE,
∴∠AED=90°,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得AE=
,解得AE= ![]() ,
,
∵HE∥BC,
∴△AHE∽△ACB,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= 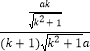 ,
,
∴AH= ![]() ,HE=
,HE= ![]() ,
,
∴CH=AC﹣AH=(k+1)a﹣ ![]() =
= ![]() a,
a,
∴tan∠HEC= ![]() =
= 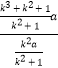 =
= ![]() ,
,
∵HE∥BC,
∴∠BCE=∠HEC,
∴tan∠ECB= ![]() .
.
【解析】(1)①作EH⊥AD于H,如图1,设CD=x,则AD=2x,AC=BC=3x,先证明△ADE为等腰直角三角形得到AH=HDF=HE=x,然后利用三角形面积公式计算出S△ADE和S△ACB , 从而得到 ![]() 的值;②在Rt△CHE中,利用正切的定义得到tan∠HEC=2,再证明∠BCE=∠HEC,所以tan∠ECB=2;(2)作EH⊥AD于H,如图2,设CD=a,则AD=ak,BC=kAC,AC=(k+1)a,BC=(k2+k)a,利用勾股定理定理计算出AB=(k+1)
的值;②在Rt△CHE中,利用正切的定义得到tan∠HEC=2,再证明∠BCE=∠HEC,所以tan∠ECB=2;(2)作EH⊥AD于H,如图2,设CD=a,则AD=ak,BC=kAC,AC=(k+1)a,BC=(k2+k)a,利用勾股定理定理计算出AB=(k+1) ![]() a,再证明△ADE∽△ABC,利用相似比得到AE=
a,再证明△ADE∽△ABC,利用相似比得到AE= ![]() ,接着证明△AHE∽△ACB,利用相似比可得到AH=
,接着证明△AHE∽△ACB,利用相似比可得到AH= ![]() ,HE=
,HE= ![]() ,则CH=
,则CH= ![]() a,则根据正切定义得到tan∠HEC=
a,则根据正切定义得到tan∠HEC= ![]() =
= ![]() ,然后证明∠BCE=∠HEC,从而得到tan∠ECB的值.
,然后证明∠BCE=∠HEC,从而得到tan∠ECB的值.
【考点精析】本题主要考查了相似三角形的性质和相似三角形的应用的相关知识点,需要掌握对应角相等,对应边成比例的两个三角形叫做相似三角形;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.