题目内容
4.如果(x+p)(x+q)=x2+mx+2(p,q为整数),则m=±3.分析 根据多项式乘以多项式法则展开,即可得出p+q=m,pq=2,根据p、q为整数得出两种情况,求出m即可.
解答 解:(x+p)(x+q)=x2+mx+2,
x2+(p+q)x+pq=x2+mx+2,
∴p+q=m,pq=2,
∵p,q为整数,
∴①p=1,q=2或p=2,q=1,此时m=3;
②p=-1,q=-2或p=-2,q=-1,此时m=-3;
故答案为:±3.
点评 本题考查了多项式乘以多项式法则的应用,能求出p、q的值是解此题的关键,注意:(a+b)(m+n)=am+an+bm+bn.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
15. 如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
 如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )| A. | 0.5米 | B. | 0.6米 | C. | 0.3米 | D. | 0.9米 |
19.下列长度的三条线段,能组成三角形的是( )
| A. | 3,6,9 | B. | 5,6,11 | C. | 5,6,10 | D. | 1,4,7 |
 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(-1,3).
 如图:已知A、B、C是数轴上的三点,点C表示的数是6,BC=4,AB=12,
如图:已知A、B、C是数轴上的三点,点C表示的数是6,BC=4,AB=12,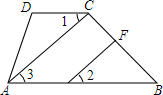 如图,在四边形ABCD中,∠BCD+∠B=180°,AC⊥CB于C,EF⊥CB于F,∠1和∠2相等吗?请完成下面的说理过程.
如图,在四边形ABCD中,∠BCD+∠B=180°,AC⊥CB于C,EF⊥CB于F,∠1和∠2相等吗?请完成下面的说理过程. 如图,该图形由6个完全相同的小正方形排列而成.
如图,该图形由6个完全相同的小正方形排列而成.