题目内容
【题目】如图,![]() 、
、![]() 、
、![]() 、
、![]() 分别为反比例函数
分别为反比例函数![]() 与
与![]() 图象上的点,且
图象上的点,且![]() 轴,
轴,![]() 轴,
轴,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() 、
、![]() .
.
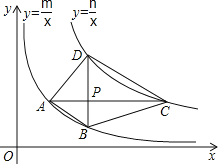
(1)若点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,请直接写出点
,请直接写出点![]() 、点
、点![]() 、点
、点![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,若四边形
,若四边形![]() 是菱形,且点
是菱形,且点![]() 的坐标为
的坐标为![]() ,请直接写出
,请直接写出![]() 、
、![]() 之间的数量关系式;
之间的数量关系式;
(3)若![]() 、
、![]() 为动点,
为动点,![]() 与
与![]() 是否相似?为什么?
是否相似?为什么?
【答案】(1)![]() 、
、![]() 、
、![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,证明详见解析.
,证明详见解析.
【解析】
(1)先利用A,B两点求出两个反比例函数的解析式,然后根据C点与A点纵坐标相同,D点与B点横坐标相同即可得到C,D的坐标,然后P的横坐标与B的横坐标相同,纵坐标与A的纵坐标相同;
(2)分别把A,C的坐标表示出来,再利用菱形的性质和点P的坐标即可求出答案;
(3)设点![]() 的坐标为
的坐标为![]() ,分别表示出点A,B,C,D的坐标,求出
,分别表示出点A,B,C,D的坐标,求出![]() 的长度,能够得出
的长度,能够得出![]() ,所以
,所以![]()
(1)解:∵点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上
上
∴![]()
∴![]()
∵![]() 轴,
轴,![]() 轴
轴
∴A,C的纵坐标相同,B,D的横坐标相同,点P的横坐标与B的横坐标相同,纵坐标与A的纵坐标相同
∴![]()
当![]() 时,代入到
时,代入到![]() 中得
中得![]() ,∴点
,∴点![]()
当![]() 时,代入到
时,代入到![]() 中得
中得![]() ,∴点
,∴点![]()
∴![]() ,
,![]() ,
,![]()
(2)∵点![]() 的坐标为
的坐标为![]()
∵![]() 轴,
轴,![]() 轴
轴
∴A,C的纵坐标与点P的纵坐标相同
当![]() 时,代入到
时,代入到![]() 中得
中得![]() ,∴点
,∴点![]()
当![]() 时,代入到
时,代入到![]() 中得
中得![]() ,∴点
,∴点![]()
∵四边形![]() 是菱形
是菱形
∴![]()
∴![]()
∴![]()
(3)解:![]()
证明:设点![]() 的坐标为
的坐标为![]()
则点![]() 的坐标为
的坐标为![]() 、点
、点![]() 的坐标为
的坐标为![]()
点![]() 的坐标为
的坐标为![]() 、点
、点![]() 的坐标为
的坐标为![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,即
,即![]()
又![]()
![]()

【题目】某公司从2016年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年度 | 投入技改资金x/万元 | 产品成本y/(万元/件) |
2016 | 2 | 18 |
2017 | 3 | 12 |
2018 | 4 | 9 |
2019 | 4.5 | 8 |
(1)根据表格中数据,求y关于x的函数解析式。
(2)在图中的网格中建立适当的平面直角坐标系,画出该函数的大致图像。
(3)如果打算在2020年让产品成本不高于7万元,则投入技改资金至少为 万元。
【题目】小明将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系,y与x的几组对应值如下表所示:
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(Ⅰ)求y关于x的函数解析式(不要求写x的取值范围);
(Ⅱ)问:小球的飞行高度能否达到22m?请说明理由.