题目内容
观察下列各式的计算结果:
1-
=1-
=
=
×
1-
=1-
=
=
×
1-
=1-
=
=
×
1-
=1-
=
=
×
…
(1)用你发现的规律填写下列式子的结果:
1-
= × ; 1-
= × ;
(2)用你发现的规律计算:
(1-
)×(1-
)×(1-
)×…×(1-
)×(1-
).
1-
| 1 |
| 22 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 32 |
| 1 |
| 9 |
| 8 |
| 9 |
| 2 |
| 3 |
| 4 |
| 3 |
1-
| 1 |
| 42 |
| 1 |
| 16 |
| 15 |
| 16 |
| 3 |
| 4 |
| 5 |
| 4 |
| 1 |
| 52 |
| 1 |
| 25 |
| 24 |
| 25 |
| 4 |
| 5 |
| 6 |
| 5 |
(1)用你发现的规律填写下列式子的结果:
1-
| 1 |
| 62 |
| 1 |
| 102 |
(2)用你发现的规律计算:
(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20132 |
| 1 |
| 20142 |
考点:有理数的混合运算
专题:规律型
分析:(1)根据平方差公式即可求解;
(2)先根据平方差公式变形,再约分计算即可求解.
(2)先根据平方差公式变形,再约分计算即可求解.
解答:解:(1)1-
=
×
;
1-
=
×
;
(2)(1-
)×(1-
)×(1-
)×…×(1-
)×(1-
)
=
×
×
×
×…×
×
=
×
=
.
故答案为:
,
;
,
.
| 1 |
| 62 |
| 5 |
| 6 |
| 7 |
| 6 |
1-
| 1 |
| 102 |
| 9 |
| 10 |
| 11 |
| 10 |
(2)(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20132 |
| 1 |
| 20142 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2013 |
| 2014 |
| 2015 |
| 2014 |
=
| 1 |
| 2 |
| 2015 |
| 2014 |
=
| 2015 |
| 4028 |
故答案为:
| 5 |
| 6 |
| 7 |
| 6 |
| 9 |
| 10 |
| 11 |
| 10 |
点评:此题考查了有理数的混合运算,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
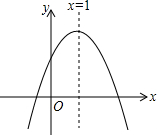 二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2-4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2-4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( )| A、2个 | B、3个 | C、4个 | D、5个 |
在Rt△ABC中,∠C=90°,AB=5,BC=2,则cosA的值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,⊙O的直径AB=10,E在⊙O内,且OE=4,则过E点所有弦中,最短弦为( )
如图,⊙O的直径AB=10,E在⊙O内,且OE=4,则过E点所有弦中,最短弦为( )| A、4 | B、6 | C、8 | D、10 |
算式(-2)÷3×(-
)的结果等于( )
| 1 |
| 3 |
A、
| ||
| B、-2 | ||
C、-
| ||
| D、2 |
若x2-2(k-1)x+4是完全平方式,则k的值为( )
| A、±1 | B、±3 |
| C、-1或3 | D、1或-32 |