题目内容
4.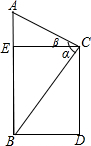 如图,在一座高为10m的大楼顶C测得旗杆底部B的俯角α为60°,测得旗杆顶端A的仰角β为20°($\sqrt{3}$≈1.73,tan20°≈0.3640)
如图,在一座高为10m的大楼顶C测得旗杆底部B的俯角α为60°,测得旗杆顶端A的仰角β为20°($\sqrt{3}$≈1.73,tan20°≈0.3640)(1)求建筑物与旗杆的水平距离BD;
(2)求旗杆高.(精确到0.1m)
分析 (1)首先根据题意分析图形;本题涉及到两个直角三角形,借助公共边CE等价转换,解这两个三角形可得BD的值;
(2)本题涉及到两个直角三角形,借助公共边CE等价转换,解这两个三角形可得AE、BE的值,再利用AB=AE+BE,进而可求出答案.
解答 解:(1)∵∠CBD=α=60°,
∴在Rt△BDC中,
tan∠CBD=$\frac{CD}{BD}$.
∴BD=$\frac{CD}{tan∠CBD}$=$\frac{10}{tan60°}$=$\frac{10}{3}$(m).
(2)设CE⊥AB,垂足为E,
∴CE=BD=$\frac{10}{3}$(m).
在Rt△AEC中,∵tanβ=$\frac{AE}{CE}$,
∴AE=CE•tanβ=$\frac{10}{3}$•tan20°≈2.1(m).
∴AB=2.1+10=12.1(m),即旗杆高为12.1m.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.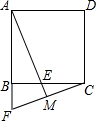 如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
 如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )| A. | BE=CE | B. | FM=MC | C. | AM⊥FC | D. | BF⊥CF |
12.已知$\frac{x}{y}$=$\frac{3}{2}$,那么下列各式不一定成立的是( )
| A. | 2x=3y | B. | $\frac{y}{x}$=$\frac{2}{3}$ | C. | $\frac{x}{2}$=$\frac{y}{3}$ | D. | $\frac{x+y}{y}$=$\frac{5}{2}$ |
9.在半径为3的⊙O,120°的圆心角所对的弧长是( )
| A. | π | B. | 2π | C. | 9π | D. | 6π |
 如图,五边形A′B′C′D′E′与五边形ABCDE是位似图形,且位似比为$\frac{1}{2}$.若五边形ABCDE的,面积为20cm2,那么五边形A′B′C′D′E′的面积为5.
如图,五边形A′B′C′D′E′与五边形ABCDE是位似图形,且位似比为$\frac{1}{2}$.若五边形ABCDE的,面积为20cm2,那么五边形A′B′C′D′E′的面积为5.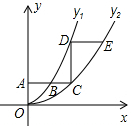 如图,平行于x轴的直线AC分别交函数y1=x2与y2=$\frac{{x}^{2}}{2}$的图象于B,C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则$\frac{DE}{AB}$=2-$\sqrt{2}$.
如图,平行于x轴的直线AC分别交函数y1=x2与y2=$\frac{{x}^{2}}{2}$的图象于B,C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则$\frac{DE}{AB}$=2-$\sqrt{2}$.