Question

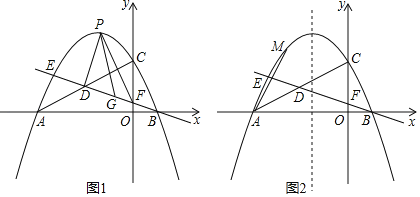
【题目】如图，正方形ECFD各顶点在Rt△ABC的边上，观察图形，并回答下列问题：

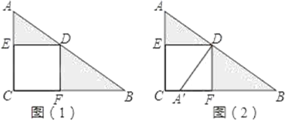
（1）请你说明由图（1）变换到图（2）的过程；

（2）若AD＝3，△AED与△BDF的面积和为9，求线段BD的长．

Answer 1

【答案】（1）△ADE绕点D逆时针旋转90°得到△A'DF；（2）BD＝6

【解析】

观察图形，发现DA旋转到，DE旋转到DF，而，由旋转的定义即可描述由图变成图的形成过程；

根据旋转的性质可得：和的面积和=的面积，即可得到，即可得到．

解：（1）∵四边形DECF为正方形，

∴∠EDF＝90°，DE＝DF，

∴DA绕点D逆时针旋转90度到的位置，DE绕点D逆时针旋转90度到DF位置，

∴△ADE绕点D逆时针旋转90°得到△A'DF；

（2）∵四边形ECFD是正方形，

∴∠CED＝∠EDF＝∠DFC＝90°，

∴∠AED＝∠DFB＝90°，∠ADE+∠FDB＝90°，

由（1）可知，△ADE≌△A'DF，

∴∠ADE＝∠A'DF，∠AED＝∠A'FD＝90°，A'D＝AD＝3，

∴∠DFB+∠A'FD＝180°，∠A'DF+∠FDB＝90°，

∴A'，F，B三点共线，

∴△AED和△BDF的面积和＝的面积，

∴A'D×BD＝9，

又∵A'D＝3，

∴BD＝6．