题目内容
 如图,将等腰直角三角形ABC绕点A逆时针旋转30°后得到△AB′C′,若AC=1,则图中阴影部分的面积是
如图,将等腰直角三角形ABC绕点A逆时针旋转30°后得到△AB′C′,若AC=1,则图中阴影部分的面积是
- A.

- B.

- C.
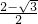
- D.3

C
分析:设BC交AB与D,由△ABC为等腰直角三角形,得到∠CAB=45°,再由旋转的性质得到∠CAC′=30°,AC=AC′=1,于是
∠C′AD=15°,在Rt△AC′D中,利用三角函数即可得到C′D=2- ,最后根据三角形的面积公式求出△AC′D的面积即图中阴影部分的面积.
,最后根据三角形的面积公式求出△AC′D的面积即图中阴影部分的面积.
解答: 解:设BC交AB于D,如图,
解:设BC交AB于D,如图,
∵△ABC为等腰直角三角形,
∴∠CAB=45°,
又∵三角形ABC绕点A逆时针旋转30°后得到△AB′C′,
∴∠CAC′=30°,AC=AC′=1,
∴∠C′AD=15°,
在Rt△PQG中,∠G=90°,∠PGQ=30°,延长GQ到M,使QM=QP,连MP,如图,
设PG=1,则QG= ,PQ=2,
,PQ=2,
∴QM=2+ ,∠M=15°,
,∠M=15°,
∴tan15°= =2-
=2- .
.
在Rt△AC′D中,
tan15°= =2-
=2- ,
,
∴C′D=2- ,
,
∴阴影部分的面积= •AC′•C′D=
•AC′•C′D= ×1×(2-
×1×(2- )=
)=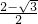 .
.
故选C.
点评:本题考查了旋转的性质,旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.同时考查了等腰三角形的性质和15度的正切值.
分析:设BC交AB与D,由△ABC为等腰直角三角形,得到∠CAB=45°,再由旋转的性质得到∠CAC′=30°,AC=AC′=1,于是
∠C′AD=15°,在Rt△AC′D中,利用三角函数即可得到C′D=2-
 ,最后根据三角形的面积公式求出△AC′D的面积即图中阴影部分的面积.
,最后根据三角形的面积公式求出△AC′D的面积即图中阴影部分的面积.解答:
 解:设BC交AB于D,如图,
解:设BC交AB于D,如图,∵△ABC为等腰直角三角形,
∴∠CAB=45°,
又∵三角形ABC绕点A逆时针旋转30°后得到△AB′C′,
∴∠CAC′=30°,AC=AC′=1,
∴∠C′AD=15°,
在Rt△PQG中,∠G=90°,∠PGQ=30°,延长GQ到M,使QM=QP,连MP,如图,

设PG=1,则QG=
 ,PQ=2,
,PQ=2,∴QM=2+
 ,∠M=15°,
,∠M=15°,∴tan15°=
 =2-
=2- .
.在Rt△AC′D中,
tan15°=
 =2-
=2- ,
,∴C′D=2-
 ,
,∴阴影部分的面积=
 •AC′•C′D=
•AC′•C′D= ×1×(2-
×1×(2- )=
)=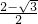 .
.故选C.
点评:本题考查了旋转的性质,旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.同时考查了等腰三角形的性质和15度的正切值.

练习册系列答案
相关题目
 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由. 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.

