题目内容
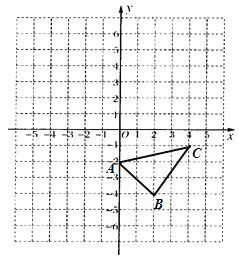
【题目】如图，在平面直角坐标系中，矩形OADB的顶点A，B的坐标分别为A（﹣6，0），B（0，4）．过点C（﹣6，1）的双曲线y=
（k≠0）与矩形OADB的边BD交于点E．
（1）填空：OA= ，k= ，点E的坐标为 ；
（2）当1≤t≤6时，经过点M（t﹣1，﹣
t2+5t﹣
）与点N（﹣t﹣3，﹣t2+3t﹣
）的直线交y轴于点F，点P是过M，N两点的抛物线y=﹣x2+bx+c的顶点．
①当点P在双曲线y=上时，求证：直线MN与双曲线y=没有公共点；
②当抛物线y=﹣x2+bx+c与矩形OADB有且只有三个公共点，求t的值；
③当点F和点P随着t的变化同时向上运动时，求t的取值范围，并求在运动过程中直线MN在四边形OAEB中扫过的面积．
【答案】（1）6，﹣6，（﹣
，4）；（2）①证明见解析；②t=
或t=
；③
.
【解析】（1）根据题意将相关数据代入.
（2）①用t表示直线MN解析式，及b，c，得到P点坐标带入双曲线y=
解析式，证明关于t的方程无解即可；
②根据抛物线开口和对称轴，分别讨论抛物线过点B和在BD上时的情况；
③由②中部分结果，用t表示F、P点的纵坐标，求出t的取值范围及直线MN在四边形OAEB中所过的面积．
解：（1）∵A点坐标为（﹣6，0）
∴OA=6
∵过点C（﹣6，1）的双曲线y=
∴k=﹣6
y=4时，x=
∴点E的坐标为（﹣，4）
故答案为：6，﹣6，（﹣，4）
（2）①设直线MN解析式为：y1=k1x+b1
由题意得：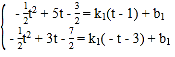
解得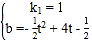
,
∵抛物线y=﹣
过点M、N,
∴
,
解得
∴抛物线解析式为：y=﹣
x2﹣x+5t﹣2
∴顶点P坐标为（﹣1，5t﹣）
∵P在双曲线y=﹣
上
∴（5t﹣）×（﹣1）=﹣6
∴t=
此时直线MN解析式为：
联立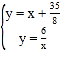
∴8x2+35x+49=0
∵△=352﹣4×8×48=1225﹣1536＜0
∴直线MN与双曲线y=﹣没有公共点．
②当抛物线过点B，此时抛物线y=﹣x2+bx+c与矩形OADB有且只有三个公共点
∴4=5t﹣2，得t=
当抛物线在线段DB上，此时抛物线与矩形OADB有且只有三个公共点
∴
，得t=
∴t=或t=
③∵点P的坐标为（﹣1，5t﹣）
∴yP=5t﹣
当1≤t≤6时，yP随t的增大而增大
此时，点P在直线x=﹣1上向上运动
∵点F的坐标为（0，﹣
）
∴yF=﹣
∴当1≤t≤4时，随者yF随t的增大而增大
此时，随着t的增大，点F在y轴上向上运动
∴1≤t≤4
当t=1时，直线MN：y=x+3与x轴交于点G（﹣3，0），与y轴交于点H（0，3）
当t=4﹣
时，直线MN过点A．
当1≤t≤4时，直线MN在四边形AEBO中扫过的面积为
S=
.
