Question

如图，由等边三角形、正方形、圆组成的轴对称图案中，等边三角形与三个正方形的面积和的比值为（   ）

A．

B．1

C．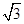

D．

Answer 1

A

解析试题分析：依题意知，过直角三角形顶点过圆心做直线垂直于底边。，图中等边三角形的高h=（设r为圆的半径），设底边边长为2x，根据勾股定理可得，（2x）²-x²=（）²，解得2x=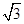r。∴等边三角形面积S₁=··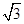=。又∵正方形的对角线等于圆的半径，所以3个正方形的面积S₂=3×2×r·r=²。∴=
考点：等边三角形，圆和正方形这类对称图形的特殊性
点评：难度较低。考查学生对几何图形的认识与灵活运算能力。运用勾股定理，等边三角形每个角
60°得出辅助线作用下的小直角为30°特殊直角三角形，30°角对应的直角边等于斜边的一半。正方形对角线把正方形平分成两个全等直角三角形等。