题目内容
如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与三个正方形的面积和的比值为( )

A. B.1 C.
B.1 C. D.
D.
【答案】
A
【解析】
试题分析:由题意知:三个正方形的共用顶点即为圆的圆心,也是等边三角形的重心;可设等边三角形的边长为2x,作等边三角形的高,再根据三角形重心的性质即可得到正方形的对角线的长;进而可求得等边三角形和正方形的面积,即可得到它们的面积比.
如图,设圆的圆心为O,过A作AD⊥BC于于D,则AD必过点O,且AO=2OD;

设△ABC的边长为2x,则 ,
, ,
,
∴正方形的边长为 ,面积为
,面积为 ,三个正方形的面积和为
,三个正方形的面积和为
△ABC的面积为
∴等边三角形与三个正方形的面积和的比值为
故选A.
考点:本题考查的是等边三角形及正方形的性质、三角形重心的性质
点评:找到等边三角形和正方形边长的比例关系是解答本题的关键.

练习册系列答案
相关题目
 如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与三个正方形的面积和的比值为( )
如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与三个正方形的面积和的比值为( )A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|






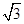


 B.1 C.
B.1 C. D.
D.