题目内容
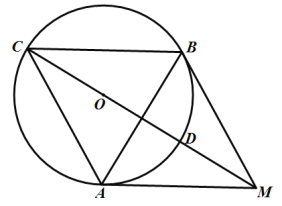
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,过点
的外接圆,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)填空:
①若![]() ,
,![]() ________;
________;
②连接![]() ,当
,当![]() 的度数为________时,四边形
的度数为________时,四边形![]() 是菱形.
是菱形.
【答案】(1)见解析;(2)①![]() ,②
,②![]() .
.
【解析】
(1)连接OA,根据圆周角定理求出∠AOC=120°,得到∠OCA的度数,根据切线的性质求出∠M的度数,根据等腰三角形的性质得到答案;
(2)①作AG⊥CM于G,根据直角三角形的性质求出AG的长,根据勾股定理求出CG,得到答案.
②证明△ABM和△ABC是等边三角形,得出AM=AC=BC=BM,即可得出结论.
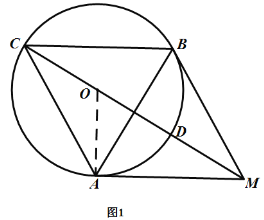
解:(1)证明:连接![]() ,如图1:
,如图1:
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)①作AG⊥CM于G,如图2: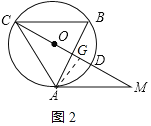
∵∠OCA=30°,AC=6,
∴AG=![]() AC=3,
AC=3,
∴CG=![]() AG=3
AG=3![]() ,
,
则MC=2CG=6![]() ;
;
故答案为:6![]() .
.
②当∠AMB的度数为60°时,四边形AMBC是菱形;理由如下:
如图3: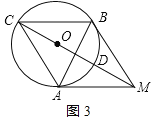
由(1)得:AM=AC,∠MAC=180°-∠AMC-∠OCA=120°,
∵∠AMB=60°,
∴∠MAC+∠AMB=180°,
∴AC∥BM,
∴∠ABM=∠BAC,
∴△ABM是等边三角形,∠BAC=∠MAC-∠MAB=60°=∠ABC,
∴AM=BM,△ABC是等边三角形,
∴BC=AC,
∴AM=AC=BC=BM,
∴四边形AMBC是菱形;
故答案为:60°.

练习册系列答案
相关题目