题目内容
17.将下列各式因式分解:(1)8x3y5-12x4y3-4x3y3
(2)9x2+30x+25
(3)x3-25x
(4)m2(a-b)+n2(b-a)
分析 (1)根据提公因式法,可得答案;
(2)根据完全平方公式,可得答案;
(3)根据提公因式法,可得平方差公式,根据平方差公式,可得答案;
(4)根据提公因式法,可得平方差公式,根据平方差公式,可得答案.
解答 解:(1)原式=4x3y3(2y2-3x-1);
(2)原式=(3x+5)2;
(3)原式=x(x2-25)=x(x+5)(x-5);
(4)原式=(a-b)(m2-n2)=(a-b)(m+n)(m-n).
点评 本题考查了因式分解,一提,二套,三检查,分解要彻底.

练习册系列答案
相关题目
7.关于方程x2-2=0的理解错误的是( )
| A. | 这个方程是一元二次方程 | |
| B. | 方程的解是$\sqrt{2}$ | |
| C. | 这个方程可以化成一元二次方程的一般形式 | |
| D. | 这个方程可以用公式法求解 |
8.有理数2016的相反数是( )
| A. | 2016 | B. | -2016 | C. | 0 | D. | -$\frac{1}{2016}$ |
10.若A(-3,y1),B(-1,y2),C(2,y3)为二次函数y=x2-2x-3的图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
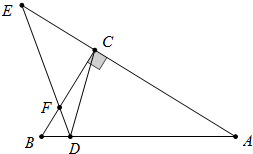 △ABC中,∠ACB=90°,AD=AC,∠CDE=45°,若BD=1,EF=2$\sqrt{5}$,则AD的长为4.
△ABC中,∠ACB=90°,AD=AC,∠CDE=45°,若BD=1,EF=2$\sqrt{5}$,则AD的长为4.