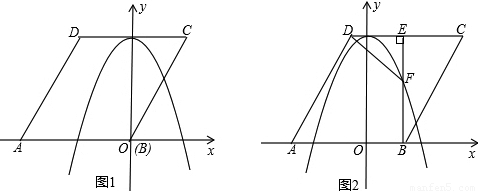题目内容
如图1,已知菱形ABCD的边长为2![]() ,点A在x轴负半轴上,点B在坐标原点.
,点A在x轴负半轴上,点B在坐标原点.
点D的坐标为(![]() ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF、AF.设菱形ABCD平移的时间为t秒(0<t<![]() )
)
①当t=1时,△ADF与△DEF是否相似?请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(写出答案即可)

解:(1)由题意得AB的中点坐标为(﹣![]() ,0),
,0),
CD的中点坐标为(0,3), …………………………2分
分别代入y=ax2+b得
![]() ,解得,
,解得,![]() ,
,
∴y=﹣x2+3. ……………………………3分
(2)①如图2所示,在Rt△BCE中,∠BEC=90°,BE=3,BC=2![]()
∴sinC=![]() =
=![]() =
=![]() ,∴∠C=60°,∠CBE=30°
,∴∠C=60°,∠CBE=30°
∴EC=![]() BC=
BC=![]() ,DE=
,DE=![]() ……………………………4分
……………………………4分
又∵AD∥BC,∴∠ADC+∠C=180°
∴∠ADC=180°﹣60°=120°……………………………5分
∵t=1,
∴B点为(1,0)
∴F(1,2) ,E(1,3)
∴EF=1 ……………………………6分
在Rt△DEF中
tan∠EDF=![]()
∴∠EDF=300
∴∠ADF=∠ADC—∠EDF=1200—300=900
∴∠ADF=∠DEF
∴DF![]() =2EF=2……………………………7分
=2EF=2……………………………7分
又∵![]() ,
,![]()
∴![]()
![]() ∴△ADF∽△DEF……………………………8分
∴△ADF∽△DEF……………………………8分
②如图3所示,依题意作出旋转后的三角形△FE′C′,过C′作MN⊥x轴,分别交抛物线、x轴于点M、点N.
观察图形可知,欲使△FE′C′落在指定区域内,必须满足:EE′≤BE且MN≥C′N.
∵F(t,3﹣t2),∴EF=3﹣(3﹣t2)=t2,∴EE′=2EF=2t2,
由EE′≤BE,得2t2≤3,解得t≤![]() .
.
∵C′E′=CE=![]() ,∴C′点的横坐标为t﹣
,∴C′点的横坐标为t﹣![]() ,
,
∴MN=3﹣(t﹣![]() )2,又C′N=BE′=BE﹣EE′=3﹣2t2,
)2,又C′N=BE′=BE﹣EE′=3﹣2t2,
由MN≥C′N,得3﹣(t﹣![]() )2≥3﹣2t2,解得t≥
)2≥3﹣2t2,解得t≥![]() .
.
∴t的取值范围为:![]() .……………………………11分
.……………………………11分





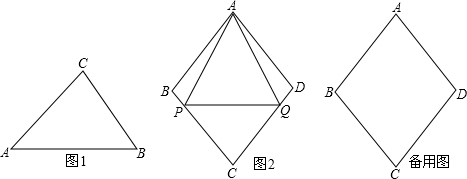
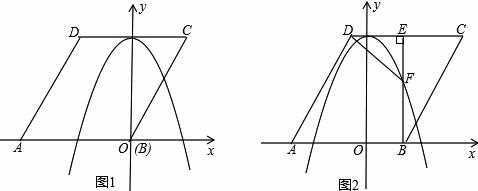
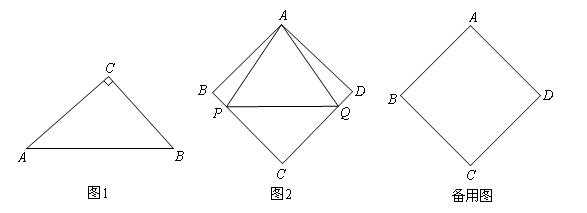
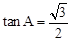 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;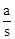 的值;
的值;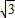 ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(- ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.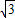 )
)