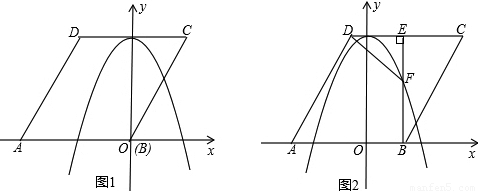题目内容
如图1,已知菱形ABCD的边长为![]() ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(- ![]() ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF、AF.设菱形ABCD平移的时间为t秒(0<t< 3 )
①是否存在这样的t,使△ADF与△DEF相似?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(写出答案即可)
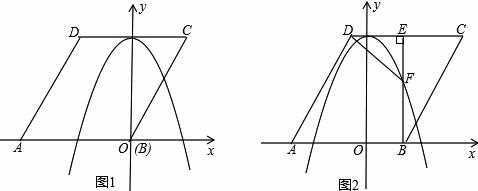
解:(1)由题意得AB的中点坐标为(-3 ,0),CD的中点坐标为(0,3),
分别代入y=ax2+b,得 ,解得,
,解得,![]() 。
。
∴这条抛物线的函数解析式为y=-x2+3。
(2)①存在。如图2所示,在Rt△BCE中,∠BEC=90°,BE=3,BC=![]() ,
,
∴![]() 。∴∠C=60°,∠CBE=30°。∴EC=
。∴∠C=60°,∠CBE=30°。∴EC=![]() BC=
BC=![]() ,DE=
,DE=![]() 。
。
又∵AD∥BC,∴∠ADC+∠C=180°。∴∠ADC=180°-60°=120°
要使△ADF与△DEF相似,则△ADF中必有一个角为直角。
(I)若∠ADF=90°,∠EDF=120°-90°=30°。
在Rt△DEF中,DE=![]() ,得EF=1,DF=2。
,得EF=1,DF=2。
又∵E(t,3),F(t,-t2+3),∴EF=3-(-t2+3)=t2。∴t2=1。
∵t>0,∴t=1 。
此时![]() ,∴
,∴![]() 。
。
又∵∠ADF=∠DEF,∴△ADF∽△DEF。
(II)若∠DFA=90°,可证得△DEF∽△FBA,则![]() 。
。
设EF=m,则FB=3-m。
∴![]() ,即m2-3m+6=0,此方程无实数根。∴此时t不存在。
,即m2-3m+6=0,此方程无实数根。∴此时t不存在。
(III)由题意得,∠DAF<∠DAB=60°,∴∠DAF≠90°,此时t不存在。
综上所述,存在t=1,使△ADF与△DEF相似。
②![]() 。
。


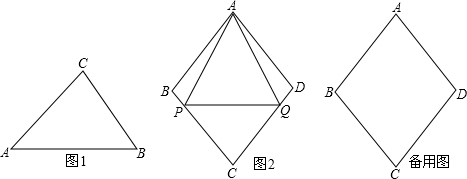
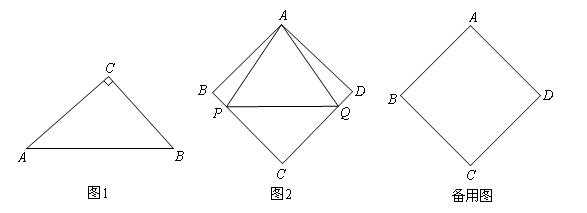
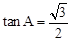 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;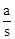 的值;
的值;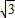 ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(- ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点. )
)