题目内容
如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.
【答案】
4cm
【解析】
试题分析:连接OC、OD,根据圆周角定理可得∠COD=60°,即可得到△COD是等边三角形,根据等边三角形的性质即可求得结果.
连接OC、OD,

则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD=4cm.
考点:圆周角定理,等边三角形的判定和性质
点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
如图,⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP︰OB=3︰5,
则CD的长为 ( )

则CD的长为 ( )

| A.6cm | B.4cm |
| C.8cm | D.10 cm |
 (2008•怀柔区二模)如图⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D.若⊙O的半径为3,则CD的长为
(2008•怀柔区二模)如图⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D.若⊙O的半径为3,则CD的长为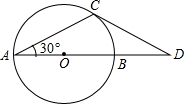 如图⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,若⊙O的半径为1,则CD的长为( )
如图⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,若⊙O的半径为1,则CD的长为( )

