题目内容
20.化简求值:$\frac{2x}{{x}^{2}-1}$÷(1-$\frac{1}{x+1}$),其中x=2cos30°•tan45°-$\sqrt{(1-\sqrt{3})^{2}}$+(-1)2017-(-$\frac{1}{2}$)-2.分析 先把原式进行化简,在根据特殊角的三角函数值求出x的值,把x的值代入化简的式子进行计算即可.
解答 解:x=2cos30°•tan45°-$\sqrt{(1-\sqrt{3})^{2}}$+(-1)2017-(-$\frac{1}{2}$)-2=2×$\frac{\sqrt{3}}{2}$×1-($\sqrt{3}$-1)-1-4=-4,
∵$\frac{2x}{{x}^{2}-1}$÷(1-$\frac{1}{x+1}$)=$\frac{2x}{(x+1)(x-1)}$•$\frac{x+1}{x}$=$\frac{2}{x-1}$,
当x=-4时,原式=-$\frac{2}{5}$.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,先把分式化简后,再把分式中未知数对应的值代入求出分式的值.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
10.将抛物线y=3x2向上平移3个单位,再向右平移2个单位,那么得到的抛物线的解析式为( )
| A. | y=3(x+2)2+3 | B. | y=3(x-2)2+3 | C. | y=3(x+2)2-3 | D. | y=3(x-2)2-3 |
11.在下列调查中,最适宜采用普查方式的是( )
| A. | 了解我市正在销售的酸奶质量情况 | |
| B. | 了解某校初三年级学生期末立定跳远成绩 | |
| C. | 了解全市中学生对雄安新区的关注程度 | |
| D. | 对全市小学生使用手机玩游戏的情况调查 |
12.商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p=$\left\{\begin{array}{l}{\frac{1}{4}t+30(1≤t≤24,t为整数)}\\{-\frac{1}{2}t+48(25≤t≤48,t为整数)}\end{array}\right.$,且其日销售量y(kg)与时间t(天)的关系如表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
| 时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
10.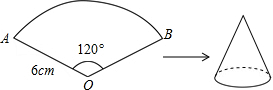 如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )
如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )
 如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )
如图已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面积为( )| A. | 4πcm2 | B. | 6πcm2 | C. | 9πcm2 | D. | 12πcm2 |
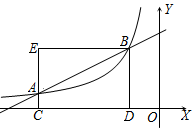 如图,已知A(m,$\frac{1}{2}$)、B(n,2)是一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的两个交点,且位于第二象限内,过A作AC⊥x轴于C,过B分别作BD⊥x轴于D,BE⊥AC于E,△ABE的面积为$\frac{9}{4}$.
如图,已知A(m,$\frac{1}{2}$)、B(n,2)是一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的两个交点,且位于第二象限内,过A作AC⊥x轴于C,过B分别作BD⊥x轴于D,BE⊥AC于E,△ABE的面积为$\frac{9}{4}$.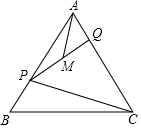 如图,在等边三角形ABC中,P为边AB上一点,Q为边AC上一点,且AP=CQ,今量得点A与线段PQ的中点M之间的距离是19cm,则点P与点C之间的距离等于38cm.
如图,在等边三角形ABC中,P为边AB上一点,Q为边AC上一点,且AP=CQ,今量得点A与线段PQ的中点M之间的距离是19cm,则点P与点C之间的距离等于38cm.