题目内容
过点(－1，7)的一条直线与x轴，y轴分别相交于点A，B，且与直线
平行．则在线段AB上，横、纵坐标都是整数的点的坐标是 ．
平行．则在线段AB上，横、纵坐标都是整数的点的坐标是 ．（1，4），（3，1）．
试题分析：平行线的解析式一次项系数相等，设直线AB为
，将点(－1，7)代入可求直线AB的解析式，根据A，B的坐标，确定x、y的取值范围求解：根据题意，设直线AB的解析式为
，由点(－1，7)在该函数图象上，得
.∴直线AB的解析式为
.∵直线
与x轴，y轴分别相交于点A，B，∴点A（
，0），B（0，
）．由0≤x≤
，且x为整数，取x=1，3时，对应的y=4，1．∴线段AB上，横、纵坐标都是整数的点的坐标是（1，4），（3，1）．
练习册系列答案
阅读快车系列答案
相关题目
．我们规定：满足不等式
的实数x的所有取值的全体叫做闭区间，表示为
．对于一个函数，如果它的自变量x与函数值y满足：当
，我们就称此函数是闭区间
是闭区间
上的“闭函数”吗？请判断并说明理由；
是闭区间
上的“闭函数”，求此函数的解析式； 
，且
，当二次函数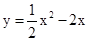
是闭区间
上的“闭函数”时，求c，d的值．
万元，这列货车挂A型车厢
节，试写出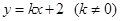
与反比例函数G1:
的图象交于点
，B（b，-1），与y轴交于点D．
，
，直接写出t的取值范围．
+bx和反比例函数
（k≠0）在同一直角坐标系中的图象如图所示，A点的坐标为（－2，0），则下列结论中，正确的是（ ）
