Question

如图，在梯形ABCD中，AD∥BC，∠BAD=90°，AD+AB=14，（AB＞AD），BD=10，BD=DC，E、F分别是BC、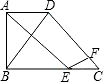CD上的点，且CE+CF=4．
（1）求BC的长；
（2）设EC的长为x，四边形AEFD的面积为y，求y关于x的函数关系式，并写出函数的定义域；
（3）在（2）的条件下，如果四边形AEFD的面积等于40，试求EC的长．

Answer 1

分析：（1）在Rt△ABD中，由AD，AB两边关系及勾股定理可求AB，AD，根据矩形性质、等腰三角形性质可求BM及BC；
（2）用相似三角形的比求△EFC的EC边上高FN，围绕y=S_梯形ABCD-S_△ABE-S_△CEF寻找条件；
（3）代值求解，把y=40，代入即可，舍去负值．

解答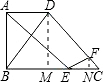：解：（1）作DM⊥BC，垂足为M，在Rt△ABD中，
∵AD+AB=14，AD²+AB²=BD²=10²，且AB＞AD，
解得AB=8，AD=6，
∵AD∥BC，∠BAD=90°
∴BM=AD=6
∵BD=DC，DM⊥BC，
∴M为BC中点，BC=2BM=12

（2）作FN⊥BC于N，设EC的长为x，则由CE+CF=4得CF=4-x
而MD=AB=8由△CNF∽△CMD可得：

FN

DM

=

CF

CD

即

FN

8

=

4-x

10

∴FN=

4(4-x)

5

∴y=S_梯形ABCD-S_△ABE-S_△CEF=

1

2

（6+12）×8-

1

2

（12-x）×8-

1

2

x×

4(4-x)

5

=

2

5

x²+

12

5

x+24，（0＜x≤4）

（3）由y=40得：

2

5

x²+

12

5

x+24=40，解得x₁=-10，（舍去）x₂=4，即EC=4．

点评：本题考查了直角梯形，矩形，等腰三角形，直角三角形的有关性质，充分运用了勾股定理，相似三角形的知识表示线段长度，运用割补法表示图形的面积，具有较强的综合性．