题目内容
不超过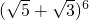 的最大整数是 ________.
的最大整数是 ________.
3903
分析:根据完全平方公式求得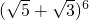 =
=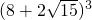 ,然后利用换元法设令
,然后利用换元法设令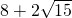 =a,
=a,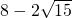 =b;经计算知,a,b是方程x2-16x+4=0的两个根,然后根据根与系数是关系解得a3、b3;再利用立方差公式解得a3+b3=16(a2+b2)-4(a+b)=3904,利用b的取值范围来解答问题.
=b;经计算知,a,b是方程x2-16x+4=0的两个根,然后根据根与系数是关系解得a3、b3;再利用立方差公式解得a3+b3=16(a2+b2)-4(a+b)=3904,利用b的取值范围来解答问题.
解答: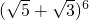 =
=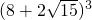 ,
,
令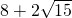 =a,
=a,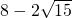 =b,
=b,
得a+b=16,ab=4,a,b是方程x2-16x+4=0的两个根,
故得a2=16a-4,b2=16b-4;
a3=16a2-4a,b3=16b2-4b;
∴a3+b3=16(a2+b2)-4(a+b)=16【16(a+b)一8】-4(a+b)=252(a+b)-128=3904.
∵0<b<1,∴0<b3<1,
∴a3的最大整数值不超过3903.
故答案是:3903.
点评:本题考查了根与系数的关系、二次根式的混合运算.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
分析:根据完全平方公式求得
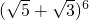 =
=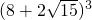 ,然后利用换元法设令
,然后利用换元法设令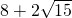 =a,
=a,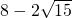 =b;经计算知,a,b是方程x2-16x+4=0的两个根,然后根据根与系数是关系解得a3、b3;再利用立方差公式解得a3+b3=16(a2+b2)-4(a+b)=3904,利用b的取值范围来解答问题.
=b;经计算知,a,b是方程x2-16x+4=0的两个根,然后根据根与系数是关系解得a3、b3;再利用立方差公式解得a3+b3=16(a2+b2)-4(a+b)=3904,利用b的取值范围来解答问题.解答:
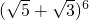 =
=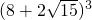 ,
,令
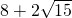 =a,
=a,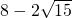 =b,
=b,得a+b=16,ab=4,a,b是方程x2-16x+4=0的两个根,
故得a2=16a-4,b2=16b-4;
a3=16a2-4a,b3=16b2-4b;
∴a3+b3=16(a2+b2)-4(a+b)=16【16(a+b)一8】-4(a+b)=252(a+b)-128=3904.
∵0<b<1,∴0<b3<1,
∴a3的最大整数值不超过3903.
故答案是:3903.
点评:本题考查了根与系数的关系、二次根式的混合运算.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的最大整数是多少?
的最大整数是多少? 的最大整数是
的最大整数是