题目内容
【题目】如图,直线y=![]() x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
(1)若MA=2,求C点的坐标;
(2)若D点的坐标为(4,0),求MC的长;
(3)当OF=MA时,直接写出点M的坐标.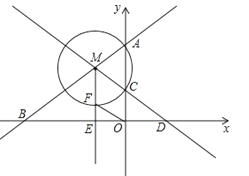
【答案】解:(1)如图1所示:过点M作MG⊥AC,垂足为G.
∵将x=0代入y=![]() x+6得y=6,
x+6得y=6,
∴A(0,6).
∴OA=6.
∵将y=0代入y=![]() x+6得
x+6得![]() x+6=0,解得:x=﹣8,
x+6=0,解得:x=﹣8,
∴B(﹣8,0)
∴OB=8.
在Rt△AOB中,由勾股定理得:AB=![]() =10.
=10.
∵∠KGA=∠BOA=90°,∠MAG=∠BAO,
∴△ABO∽△AMG.
∴![]() ,即
,即![]() ,解得:AG=1.2.
,解得:AG=1.2.
∵MG⊥AC,AM=MC,
∴AG=CG=1.2.
∴AC=2.4.
∴OC=OA﹣AC=6﹣2.4=3.6.
∴C(0,3.6).
(2)如图2所示:过点M作MG⊥AC,垂足为G.
∵∠OCD=∠MCA,∠MCA=∠MAC,
∴∠OCD=∠BAO.
又∵∠BOA=∠DOC,
∴△DOC∽△BOA.
∴![]() =
=![]() ,即
,即![]() ,解得OC=3.
,解得OC=3.
∵由(1)可知AG=![]() AC,
AC,
∴AG=![]() X(OA-OC)=
X(OA-OC)=![]() .
.
∵由(1)可知△ABO∽△AMG,
∴![]() ,即
,即![]() ,解得:AM=
,解得:AM=![]() .
.
∵MC=AM,
∴MC=![]() .
.
(3)①如图3所示:过点M作MG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H.
∵由(2)可知△DOC∽△BOA,
∴∠MBD=∠MDB.
∴MB=MD.
又∵E是BD的中点,
∴ME⊥BD.
∴四边形FMGH为矩形.
在Rt△MAG和Rt△FOH中,![]() ,
,
∴Rt△MAG≌Rt△FOH.
∴AG=OH=![]() AM.
AM.
∵AG+GH+OH=6,
∴![]() AM+AM+
AM+AM+![]() AM=6.
AM=6.
解得:AM=![]() .
.
∴AG=![]() X
X![]() =
=![]() ,OH=
,OH=![]() AM+AM=
AM+AM=![]() X
X![]() +
+![]() =
=![]() .
.
∴点M的坐标为(﹣![]() ,
,![]() ).
).
②如图4所示:过点M作MG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H.
由①可知四边形MGHF为矩形.
在Rt△MAG和Rt△FOH中,![]() ,
,
∴Rt△MAG≌Rt△FOH.
∴∠MAG=∠FOH.
∴MA∥OF.
又∵MF∥AC,
∴四边形AOFM是平行四边形.
∴MF=AC=6.
∴AM=6.
∴GM=6X![]() =
=![]() ,AG=6×
,AG=6×![]() =
=![]() .
.
∴OG=OA﹣AG=6﹣![]() =
=![]() .
.
∴点M的坐标为(﹣![]() ,
,![]() ).
).
【解析】(1)过点M作MG⊥AC,垂足为G.先求得点A和点B的坐标,然后求得AB的长,接下来证明△ABO∽△AMG,依据相似三角形的性质可求得AG=1.2,依据等腰三角形三线合一的性质可求得AC的长,从而得到点C的坐标
(2)过点M作MG⊥AC,垂足为G.先证明△DOC∽△BOA,从而可求得OC=3,然后由△ABO∽△AMG可求得AM的长,从而得到MC的长;
(3)①过点M作MG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H.先证明△MBD为等腰三角形,依据等腰三角形三线合一的性质可证明MF⊥BD,从而得到四边形FMGH为矩形,然后再证明Rt△MAG≌Rt△FOH,从而得到AG=OH=![]() AM,可求得AM的长,由AM的长可求得AG、MG的长,故此可求得点M的坐标;②过点M作MG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H.先证明Rt△MAG≌Rt△FOH,于是得到∠MAG=∠FOH,接下来可证明四边形AOFM是平行四边形,故此可求得AM=6,从而可求得点M的坐标.
AM,可求得AM的长,由AM的长可求得AG、MG的长,故此可求得点M的坐标;②过点M作MG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H.先证明Rt△MAG≌Rt△FOH,于是得到∠MAG=∠FOH,接下来可证明四边形AOFM是平行四边形,故此可求得AM=6,从而可求得点M的坐标.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案