题目内容
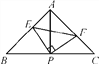
【题目】如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM,请你判断△OMN的形状,并说明理由.

【答案】△OMN是等腰直角三角形.理由见解析.
【解析】
试题分析:连接OA.先证得△OAN≌△OBM,然后根据全等三角形的对应边相等推知OM=ON;然后由等腰直角三角形ABC的性质、等腰三角形OMN的性质推知∠NOM=90°,即△OMN是等腰直角三角形.
试题解析:△OMN是等腰直角三角形.
理由:连接OA.
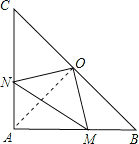
∵在△ABC中,∠A=90°,AB=AC,O是BC的中点,
∴AO=BO=CO(直角三角形斜边上的中线是斜边的一半);
∠B=∠C=45°;
在△OAN和OBM中,
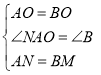
∴△OAN≌△OBM(SAS),
∴ON=OM;
∴∠AON=∠BOM;
又∵∠BOM+∠AOM=90°,
∴∠NOM=∠AON+∠AOM=90°,
∴△OMN是等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目