Question

某班数学兴趣小组为了测量建筑物AB与CD的高度，他们选取了地面上点E和建筑物CD的顶端点C为观测点，已知在点C处测得点A的仰角为45°；在点E处测得点C的仰角为30°，测得点A的仰角为37°．又测得DE的长度为9米．
（1）求建筑物CD的高度；
（2）求建筑物AB的高度．
（参考数据：≈1.73，sin37°≈，cos37°≈，tan37°≈）

Answer 1

解：（1）在Rt△CDE中，
∵tan∠CED=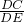，DE=9，∠CED=30°，
∴tan30°=，DC=3≈5.19，
答：建筑物CD的高度为5.19米．

（2）过点C作CF⊥AB于点F．
在Rt△AFC中，
∵∠ACF=45°，
∴AF=CF．
设AF=x米，在Rt△ABE中，AB=3+x，BE=9+x，∠AEB=37°，
tan∠AEB=，
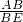tan37°=≈，
解得：x≈6.24，
则AB=3+x≈11.43．
答：建筑物AB的高度为11.43米．
分析：（1）根据锐角三角函数关系得出tan∠CED=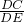，即可求出DC的长度；
（2）根据过点C作CF⊥AB于点F，利用tan∠AEB=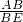，求出AF的长即可得出AB的长．
点评：此题主要考查了仰角与俯角问题，根据已知构造直角三角形进而得出DC与AF的长是解题关键．