��Ŀ����
��ͼ��������y=��x2��2x+3��x�ύ�ڵ�A��B������������x�ἰ���Ϸ��IJ��ּ���C1����C1���ڵ�B�����ĶԳƵ�C2��C2��x�ύ����һ��C����C2���ڵ�C�����ĶԳƵ�C3������C1��C3�Ķ��㣬��ͼ����Ӱ���ֵ����Ϊ_____��

���𰸡�32
�������������������������y=��x2��2x+3��x�ύ�ڵ�A��B��
�൱y=0ʱ����x2��2x+3=0��
���x=��3��x=1��
��A��B������ֱ�Ϊ����3��0������1��0����
AB�ij���Ϊ4��
��C1��C3�������ֶ���ֱ����������߽�x����E��F���㣮
�������ĶԳƵ����ʣ�x���·����ֿ����ضԳ���ƽ���ֳ������ֲ���C1��C2��
��ͼ��ʾ����Ӱ����ת��Ϊ���Σ�

���ݶԳ��ԣ��ɵ�BE=CF=4��2=2����EF=8
�����䷽���ɵ�y=��x2��2x��3=����x+1��2+4
������Ϊ����1��4��������Ӱ���ֵĸ�Ϊ4��
S��=8��4=32��
���㣺��������x��Ľ��㣮
�����͡������
��������
17
�ⷽ�̣���1��2��3x��1��=16����2�� ����3��
����3�� ��
��
��ϰ��ϵ�д�
�����Ŀ


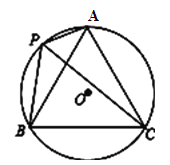
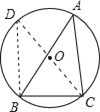
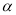 �Ͱӵ�AD.������������ţ�
�Ͱӵ�AD.������������ţ�
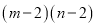 �� ����
�� ����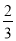 ����BC�ij���
����BC�ij���
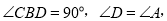
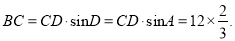
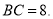
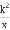 ��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��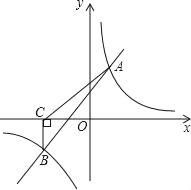
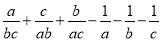 =_____��
=_____��