题目内容
 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.分析:先根据AB⊥OC′,OS⊥OC′可知△ABC∽△SOC,同理可得△A′B′C′∽△SOC′,再由相似三角形的对应边成比例即可得出h的值.
解答:解:∵AB⊥OC′,OS⊥OC′,
∴SO∥AB,
∴△ABC∽△SOC,
∴
=
,即
=
,
解得OB=
h-1①,
同理,∵A′B′⊥OC′,
∴△A′B′C′∽△SOC′,
∴
=
,
=
②,
把①代入②得,
=
,
解得h=9(米).
答:路灯离地面的高度是9米.
∴SO∥AB,
∴△ABC∽△SOC,
∴
| BC |
| BC+OB |
| AB |
| OS |
| 1 |
| 1+OB |
| 1.5 |
| h |
解得OB=
| 2 |
| 3 |
同理,∵A′B′⊥OC′,
∴△A′B′C′∽△SOC′,
∴
| B′C′ |
| B′C′+BB′+OB |
| A′B′ |
| OS |
| 1.8 |
| 1.8+4+OB |
| 1.5 |
| h |
把①代入②得,
| 1.8 | ||
5.8+
|
| 1.5 |
| h |
解得h=9(米).
答:路灯离地面的高度是9米.
点评:本题考查的是相似三角形在实际生活中的应用,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目

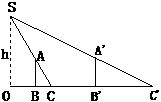
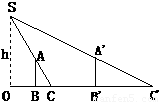
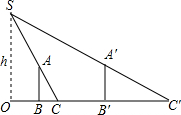 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.