题目内容
 如图,E、F是?ABCD的对角线BD上两点,且DE=BF.若∠AED=110°,∠ABD=25°,则∠DCF的度数为________.
如图,E、F是?ABCD的对角线BD上两点,且DE=BF.若∠AED=110°,∠ABD=25°,则∠DCF的度数为________.
85°
分析:首先由BF=DE可以得到BE=DF,然后利用平行四边形性质可以得到AB=CD,AB∥CD,接着利用平行线的性质可以得到∠ABD=∠CDB,利用全等三角形的判定方法即可得到△ABE≌△CDF,从而得到∠DFC=∠AEB,再根据条件∠AED=110°,求出∠DFC=∠AEB=70°后,即可根据三角形内角和为180°求的答案.
解答:∵BF=DE,
∴BF+EF=DE+EF,
即BE=DF,
∵?ABCD中,AB=CD,AB∥CD,
∴∠ABD=∠CDB=25°,
∴△ABE≌△CDF,
∴∠DFC=∠AEB,
∵∠AED=110°,
∴∠DFC=∠AEB=180°-110°=70°,
∴∠DCF=180°-25°-70°=85°.
故答案为:85°.
点评:此题主要考查了平行四边形的性质,同时也考查了三角形全等的判定,解题的关键是利用平行四边形的性质得到全等三角形.
分析:首先由BF=DE可以得到BE=DF,然后利用平行四边形性质可以得到AB=CD,AB∥CD,接着利用平行线的性质可以得到∠ABD=∠CDB,利用全等三角形的判定方法即可得到△ABE≌△CDF,从而得到∠DFC=∠AEB,再根据条件∠AED=110°,求出∠DFC=∠AEB=70°后,即可根据三角形内角和为180°求的答案.
解答:∵BF=DE,
∴BF+EF=DE+EF,
即BE=DF,
∵?ABCD中,AB=CD,AB∥CD,
∴∠ABD=∠CDB=25°,
∴△ABE≌△CDF,
∴∠DFC=∠AEB,
∵∠AED=110°,
∴∠DFC=∠AEB=180°-110°=70°,
∴∠DCF=180°-25°-70°=85°.
故答案为:85°.
点评:此题主要考查了平行四边形的性质,同时也考查了三角形全等的判定,解题的关键是利用平行四边形的性质得到全等三角形.

练习册系列答案
相关题目
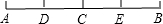


 20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE.
20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE. (2013•荣昌县模拟)如图,⊙O的直径是AB,∠C=35°,则∠DAB的度数是( )
(2013•荣昌县模拟)如图,⊙O的直径是AB,∠C=35°,则∠DAB的度数是( )