题目内容
先化简,再求值(10分)
 ,其中
,其中 .
.
化简得原式=x-1,x= ,原式的值为
,原式的值为 .
.
【解析】
试题分析:根据分式的运算法则,先对代数式进行化简,根据x对应的代数式进行化简,然后把x的值代入化简所得的代数式,进行计算即可.
试题解析:【解析】
原式=
 ,
,
 ,∴原式
,∴原式 .
.
考点:代数式的化简求值;特殊角的三角函数值.
考点分析: 考点1:分式 分式:中考试题中分值约为6-8分,主要以填空,简答计算题型出现,难易度属于中。近几年主要考察①分式的概念,性质,意义②分式的运算,化简求值。③列分式方程解决实际问题、突破方法:①掌握并灵活应用分式的基本性质,②在通分和约分时,都要注意分解因式知识的应用。③化简求值时,注意整体思想和技巧的应用。④留意生活中是实际问题 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
某林业部门要考查某种幼树在一定条件的移植成活率.在同样条件下,大量地对这种幼树进行移植,并统计成活情况,计算成活的频率.如下表:
移植总数(n) | 成活数(m) | 成活的频率 |
10 | 8 | 0.80 |
50 | 47 | 0.94 |
270 | 235 | 0.870 |
400 | 369 | 0.923 |
750 | 662 | 0.883 |
1500 | 1335 | 0.89 |
3500 | 3203 | 0.915 |
7000 | 6335 | 0.905 |
9000 | 8073 | 0.897 |
14000 | 12628 | 0.902 |
所以可以估计这种幼树移植成活的概率为( )
(A)0.1 (B)0.2 (C)0.8 (D)0.9
 ,若
,若 为
为 中点,则
中点,则 = .
= .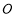 相切于E,F,G三点,且AB∥CD,连接OB,OC.
相切于E,F,G三点,且AB∥CD,连接OB,OC. 的半径及MN的长.
的半径及MN的长.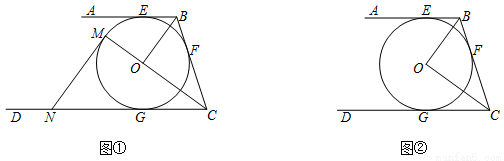

 ,
, 满足
满足 ,则
,则 的值是 .
的值是 .
 ,其中
,其中 是方程
是方程 的根.
的根.



