题目内容
点O是△ABC的内心,过点O作EF∥AB,分别与AC、BC交于点E、F, AE=3、BF=2.5则EF= .
EF=5.5
解析试题分析:根据等腰三角形性质及三角形内心求得,连接OA,OB,∵EF∥AB, ∠EOA∠BAO, ∠OBA=∠FOB,又∵点O是△ABC的内心,∴∠EOA=∠EAO, ∠OBA=∠BOF,∴AO=EO,BO=OF.∴EF=5.5.
考点:等腰三角形性质,三角形内接圆定义。
点评:熟练掌握上述性质定义,在解答时由已知易求之,本题属于基础题。

练习册系列答案
相关题目
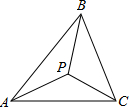 如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB的度数为( )
如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB的度数为( )| A、150° | B、120° | C、90° | D、60° |
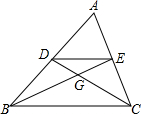 如图,△ABC的中线BE与CD交于点G,连结DE,下列结论正确的是( )
如图,△ABC的中线BE与CD交于点G,连结DE,下列结论正确的是( )| A、点G是△ABC的内心 | B、BD=2CE | C、S△BGC=2S△DGE | D、S△BDG=S△CEG |
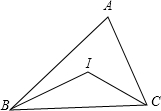 如图,在△ABC中,∠A=68°,点I是△ABC的内心,则∠BIC的度数为
如图,在△ABC中,∠A=68°,点I是△ABC的内心,则∠BIC的度数为 如图,若点O是△ABC的内心,∠ABC=80°,∠ACB=60°则∠BOC的度数为( )
如图,若点O是△ABC的内心,∠ABC=80°,∠ACB=60°则∠BOC的度数为( )