题目内容
 直角梯形ABCD中,AB∥CD,∠C=90°,AB=BC,M为BC边上一点.
直角梯形ABCD中,AB∥CD,∠C=90°,AB=BC,M为BC边上一点.
(1)若∠DMC=45°,求证:AD=AM.
(2)若∠DAM=45°,AB=7,CD=4,求BM的值.
 (1)证明:作AF⊥CD交延长线于点F.
(1)证明:作AF⊥CD交延长线于点F.∵∠DMC=45°,∠C=90°
∴CM=CD,
又∵∠B=∠C=∠AFD=90°,AB=BC,
∴四边形ABCF为正方形,
∴BC=CF,
∴BM=DF,
在Rt△ABM和Rt△AFD中,
 ,
,∴△ABM≌△AFD(SAS),
∴AD=AM.
(2)解:把Rt△ABM绕点A顺时针旋转90°,使AB与AF重合,得Rt△AFN.
∵∠DAM=45°,
∴∠BAM+∠DAF=45°,
由旋转知∠BAM=∠NAF,
∴∠DAF+∠NAF=45°,
即∠DAM=∠DAN,
由旋转知AM=AN,
∴△ADM≌△ADN,
∴DM=DN,
设BM=x,
∵AB=BC=CF=7,
∴CM=7-x
又∵CD=4,
∴DF=3,BM=FN=x,
∴MD=DN=3+x,
在Rt△CDM中,(7-x)2+42=(3+x)2,
解得:x=
 .
.∴BM的值为
 .
.答:BM的值为
 .
.分析:(1)作AF⊥CD交延长线于点F,根据∠DMC=45°,∠C=90°,得到∠B=∠C=∠AFD=90°,AB=BC,推出正方形ABCF,根据正方形的性质得到BC=CF,进一步证出△ABM≌△AFD,即可得到答案;
(2)把Rt△ABM绕点A顺时针旋转90°,使AB与AF重合,得Rt△AFN,由已知∠DAM=45°和旋转,推出∠DAM=∠DAN,得到△ADM≌△ADN,设BM=x,得到CM=7-x,BM=FN=x,MD=DN=3+x,在Rt△CDM中,根据勾股定理即可求出答案.
点评:本题主要考查对直角梯形,全等三角形的性质和判定,正方形的性质和判定,勾股定理,垂线,旋转的性质,解一元二次方程等知识点的理解和掌握,此题是一个拔高的题目,有一定的难度.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
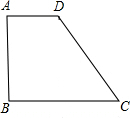 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为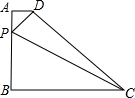 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为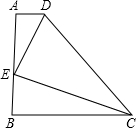 下结论:
下结论: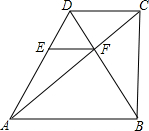 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.