题目内容
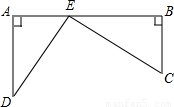
(6分)铁路上A, B两站(两站间视为直线),相距25km,C,D为两村庄(视为两个点),DA⊥AB于A,CB⊥AB于B(如图),已知DA="15km,CB=10km," 现在要在铁路AB上建设一个土特产品收购站E,使得C,D两村庄到E站距离相等,则E站应建在距离A站多远处? 
【答案】
E站应建在距离A站10米处。
【解析】
试题分析:因为DA⊥AB于A,CB⊥AB于B,在两个直角三角形AED和EBC中,需要斜边相等,可以利用勾股定理得出斜边,那我们未知数AE=x,利用勾股定理
DE= 
CE= 
因为DE="CE,"
 ,代入得一元一次方程
,代入得一元一次方程




所以,E站应建在距离A站10米处。
考点:勾股定理,解一元一次方程
点评:难度系数中等,综合运用题目,理解好题意,利用两个直角三角形的斜边相等,用勾股定理联系起来,并利用一元一次方程,解出答案。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
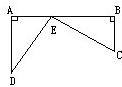 16、铁路上A、B两站(视为直线上两点)相距25km,C、D为两村庄(视为两个点),DA⊥AB于A,CB⊥AB于B(如图),已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站
16、铁路上A、B两站(视为直线上两点)相距25km,C、D为两村庄(视为两个点),DA⊥AB于A,CB⊥AB于B(如图),已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站 如图,铁路上A、B两站相距25千米,C、D两村庄视为两点,DA⊥AB于A,CB⊥AB于B,已知DA=15千米,CB=10千米,现要在铁路AB上修一个土特产品收购站E,收购站E到C、D两村庄的距离和最小值为( )
如图,铁路上A、B两站相距25千米,C、D两村庄视为两点,DA⊥AB于A,CB⊥AB于B,已知DA=15千米,CB=10千米,现要在铁路AB上修一个土特产品收购站E,收购站E到C、D两村庄的距离和最小值为( )