题目内容
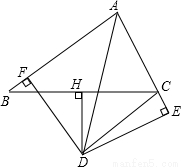
(本小题满分9分)如图,在矩形ABCD中,E是CD边上一动点,设DE=x,作AF⊥AE交CB的延长线于点F.

(1)当点E不与点C,D重合时,求证:△ADE∽△ABF;
(2)连接EF,M为EF的中点,AB=4,AD=2, 当点E从D运动到C的过程中
①点M经过的路径是( )
A. 直线 B. 线段 C. 射线 D. 圆弧
②求点M经过的路径的长;
③连接BM,直接写出BM的长度的最小值.
【解析】
试题分析:(1)根据矩形得出∠D=∠ABF=90°,根据垂直得出∠DAE=∠BAF,从而说明全等;(2)首先画出极端的两种情况,再看点M的位置关系;我们首先设DE=x,取CF的中点H,连接MH,BM,根据△ADE∽△ABF,得出BF=2x,FC=2+2x,FH=1+x,根据直角△MHB的勾股定理得出BM的二次函数关系式,然后根据二次函数的性质进行求解.
试题解析:(1)∵在矩形ABCD中,∠DAB=∠ABC=∠C=∠D=90°, ∴∠ABF=∠D=90°,
∵AF⊥AE, ∴∠EAF=∠BAF+∠EAB=90°, ∵∠DAE+∠EAB=∠DAB=90°, ∴∠DAE=∠BAF,
∴△ADE∽△ABF;
(2)①、B ②、点M所运动的路程长度等于矩形的对角线长度,则点M运动的长度=2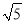
③、BM的最小值为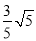
考点:三角形相似的应用
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目

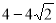 ,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.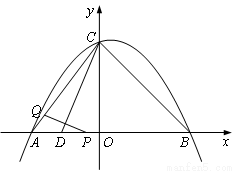
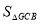 =
=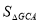 ,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.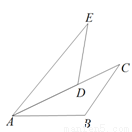

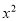 -(m+3)x+m+2=0的两个根,求△ABC的周长.
-(m+3)x+m+2=0的两个根,求△ABC的周长.