题目内容
函数y=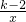
，当x＞0时，y随x的增大而增大，则
- A.k＞0
- B.k＜2
- C.k＜0
- D.k＞2
B
分析：利用反比例函数的增减性可得出k-2＜0，再求解即可得出k的取值范围．
解答：∵函数y=，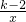
当x＜0时，y随x的增大而增大，
∴k-2＜0，即k＜2．
故选B．
点评：本题考查反比例函数的性质：①当k＞0时，在同一个象限内，y随x的增大而减小；②当k＜0时，在同一个象限，y随x的增大而增大；
分析：利用反比例函数的增减性可得出k-2＜0，再求解即可得出k的取值范围．
解答：∵函数y=
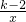，当x＜0时，y随x的增大而增大，
∴k-2＜0，即k＜2．
故选B．
点评：本题考查反比例函数的性质：①当k＞0时，在同一个象限内，y随x的增大而减小；②当k＜0时，在同一个象限，y随x的增大而增大；
练习册系列答案
中考解读考点精练系列答案
相关题目
下列函数中，当x＞0时，y随x的增大而增大的函数是（ ）
| A、y=-x2+2 | ||
B、y=
| ||
| C、y=-3x | ||
| D、y=2x+1 |
下列函数中，当x＞0时，y随x的增大而减小的是（ ）
| A、y=2x | ||
| B、y=2x-1 | ||
C、y=
| ||
| D、y=-2x2 |
（2010•路南区三模）已知，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，BD平分∠ABC，交AC于点D．动点P从D点出发沿DC向终点C运动，速度为每秒1个单位，动点Q从B点出发沿BA向终点A运动，速度为每秒4个单位．两点同时出发，当一点到达终点时，两点停止运动．设P、Q运动时间为t秒．