题目内容
 (2010•路南区三模)已知,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,BD平分∠ABC,交AC于点D.动点P从D点出发沿DC向终点C运动,速度为每秒1个单位,动点Q从B点出发沿BA向终点A运动,速度为每秒4个单位.两点同时出发,当一点到达终点时,两点停止运动.设P、Q运动时间为t秒.
(2010•路南区三模)已知,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,BD平分∠ABC,交AC于点D.动点P从D点出发沿DC向终点C运动,速度为每秒1个单位,动点Q从B点出发沿BA向终点A运动,速度为每秒4个单位.两点同时出发,当一点到达终点时,两点停止运动.设P、Q运动时间为t秒.(1)求线段CD的长;
(2)求△BPQ的面积S与t之间的函数关系式;当S=7.2时,求t的值;
(3)在点P、点Q的移动过程中,如果将△APQ沿其一边所在直线翻折,翻折后的三角形与△APQ组成一个四边形,直接写出使所组成的四边形为菱形的t的值.
分析:(1)过点D作DE⊥AB于E,由角平分线的性质定理就可以得出DE=DC,BE=BC=6,由勾股定理可以求出AB,设出CD=x,则可以表示出AD、BE,由勾股定理就可以求出x.
(2)作QF⊥AC于F,可以这么三角形相似把QF用含t的式子表示出来,而S△BPQ=S△ABC-S△AQP-S△PCB,就可以表示出积S与t之间的函数关系式.
(3)当BQ=BP时利用勾股定理建立等量关系就可以求出其t值,当BP=QP时,作PM⊥AB,根据等腰三角形的性质就可以求出其t值;当PQ=BQ时,作QN⊥AC,利用三角形相似就可以求出其t值.
(2)作QF⊥AC于F,可以这么三角形相似把QF用含t的式子表示出来,而S△BPQ=S△ABC-S△AQP-S△PCB,就可以表示出积S与t之间的函数关系式.
(3)当BQ=BP时利用勾股定理建立等量关系就可以求出其t值,当BP=QP时,作PM⊥AB,根据等腰三角形的性质就可以求出其t值;当PQ=BQ时,作QN⊥AC,利用三角形相似就可以求出其t值.
解答:解:(1)过点D作DE⊥AB于E,
∵BD平分∠ABC,∠ACB=90°,
∴DE=DC,
∴△BDE≌△BDC,
∴BE=BC,在Rt△ABC中,由勾股定理,得
AB=
=10,
设CD=x,则AD=8-x,DE=x,
∴16+x2=(8-x)2,
∴x=3,
∴CD=3.

(2)作QF⊥AC于F,
∴∠AFQ=90°,
∵∠ACB=90°,
∴QF∥BC,
∴△AQF∽△ABC,
∴
=
,
∴
=
,
∴QF=
,
∴S△BPQ=
×6×8-
-
(5+t)•
,
∴S=
t2+6t,
当S=7.2时,
7.2=
t2+6t,
解得,t1=-6(舍去),t2=1;

(3)当AQ=AP时,BQ=4t,CP=3-t,在Rt△BPC中,由勾股定理,得
16t2=(3-t)2+36,
解得x1=
(舍去),x2=
;
当AP=PQ时,t1=1,t2=
;
当PQ=AQ时,不存在.
∴t的值为:
,1,
.

∵BD平分∠ABC,∠ACB=90°,
∴DE=DC,
∴△BDE≌△BDC,
∴BE=BC,在Rt△ABC中,由勾股定理,得
AB=
| 36+64 |
设CD=x,则AD=8-x,DE=x,
∴16+x2=(8-x)2,
∴x=3,
∴CD=3.

(2)作QF⊥AC于F,
∴∠AFQ=90°,
∵∠ACB=90°,
∴QF∥BC,
∴△AQF∽△ABC,
∴
| AQ |
| AB |
| QF |
| BC |
∴
| 10-4t |
| 10 |
| QF |
| 6 |
∴QF=
| 30-12t |
| 5 |
∴S△BPQ=
| 1 |
| 2 |
| 6×(3-t) |
| 2 |
| 1 |
| 2 |
| 30-12t |
| 5 |
∴S=
| 6 |
| 5 |
当S=7.2时,
7.2=
| 6 |
| 5 |
解得,t1=-6(舍去),t2=1;

(3)当AQ=AP时,BQ=4t,CP=3-t,在Rt△BPC中,由勾股定理,得
16t2=(3-t)2+36,
解得x1=
-1-2
| ||
| 5 |
-1+2
| ||
| 5 |
当AP=PQ时,t1=1,t2=
| 15 |
| 7 |
当PQ=AQ时,不存在.
∴t的值为:
-1+2
| ||
| 5 |
| 15 |
| 7 |

点评:本题考查了轴对称,三角形的面积,两点间的距离,菱形的判定及性质,勾股定理的运用,相似三角形的判定及性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2010•路南区三模)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=20°,那么∠2的度数等于( )
(2010•路南区三模)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=20°,那么∠2的度数等于( )
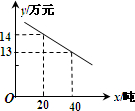 (2)根据题中条件和(1)的结果,求年利润w甲(万元)与x(吨)之间的函数关系式和甲的最大年利润;
(2)根据题中条件和(1)的结果,求年利润w甲(万元)与x(吨)之间的函数关系式和甲的最大年利润;