题目内容
某市政府大力扶持大学生创业,李明在政府的扶持下投资销售一种进价为每件50元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+900.
(1)设李明每月获得利润为w(元),求w关于x的函数关系式,并写出自变量x的取值范围;
(2)如果李明想要每月获得最大月利润,那么他的销售单价应定为多少元?此时的月成本为多少元?
(3)若物价部门规定这种护眼台灯的销售单价不得超过75元,李明想使获得的月利润不低于3000元,他应给销售单价确定怎样的范围?
解:(1)由题意,得:w=(x-50)×y=(x-50)•(-10x+900)=-10x2+1400x-45000,
自变量x的取值范围:90>x>50
(2)x=![]() =70,w=(70-50)•(-10×70+900)=4000,200×50=10000
=70,w=(70-50)•(-10×70+900)=4000,200×50=10000
答:当销售单价定为70元时,每月可获得最大利润,此时的月成本为10000元
(3)∵a=-10<0,
∴抛物线开口向下,
∴当60≤x≤80时,w≥3000,
∵x≤75,
∴当60≤x≤75时,w≥3000,
答:他应给销售单价确定在60≤x≤75.

练习册系列答案
相关题目
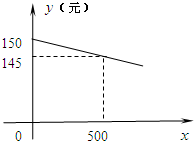 某市政府大力扶持大学生创业.张涛在政府的扶持下销售一种进价为每件20元的新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.
某市政府大力扶持大学生创业.张涛在政府的扶持下销售一种进价为每件20元的新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.