题目内容
根据下列线段图，你能写出一个符合条件的生活的事例吗？
解：例如：甲，乙二人从A地出发，甲的速度是每小时6千米，乙的速度是每小时4千米，甲在乙先出发10千米后再出发，那么几小时后甲才能追上乙？
解：设x小时后甲才能追上乙，
则有：6x=10+4x，
解得：x=5，
即5小时后甲才能追上乙．
分析：由图可看出：可以选择路程问题中的同向而行问题．
点评：此题是数形结合题，要密切联系生活实际．
解：设x小时后甲才能追上乙，
则有：6x=10+4x，
解得：x=5，
即5小时后甲才能追上乙．
分析：由图可看出：可以选择路程问题中的同向而行问题．
点评：此题是数形结合题，要密切联系生活实际．
练习册系列答案
相关题目
在某校组织的社会实践活动中，小明同学到某超市进行了一项社会调查，发现有一种水果1-6月份售价y（元/kg）与时间t（月）的关系可用一条线段上的点来表示，如图所示，该水果的成本m（元/kg）与时间t（月）满足二次函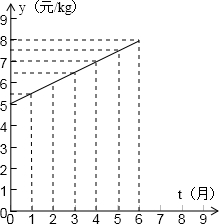
数关系，相应的数据如表所示．根据图象提供的信息，解答下列问题：
（1）求售价y（元/kg）与时间t（月）之间的函数关系式．
（2）求表中成本m（元/kg）与时间t（月）之间的函数关系式．
（3）你能求出每千克水果的利润W（元/kg）与时间t（月）之间的函数关系式吗？若该超市在1-6月份每月都销售水果3000kg，请问一个月内最多获利多少元？
数关系，相应的数据如表所示．根据图象提供的信息，解答下列问题：（1）求售价y（元/kg）与时间t（月）之间的函数关系式．
（2）求表中成本m（元/kg）与时间t（月）之间的函数关系式．
（3）你能求出每千克水果的利润W（元/kg）与时间t（月）之间的函数关系式吗？若该超市在1-6月份每月都销售水果3000kg，请问一个月内最多获利多少元？
| t（月） | 1 | 2 | 3 | … | ||||
| m（元/kg） |
|
|
3 | … |
