题目内容
已知:同圆的内接正三角形与内接正方形的边长之比为
:
:
.
| 3 |
| 2 |
| 3 |
| 2 |
分析:根据题意画出图形,设出圆的半径,再由正多边形及直角三角形的性质求解即可.
解答: 解:设圆的半径为R,
解:设圆的半径为R,
如图(一),连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB•cos30°=
R,
故BC=2BD=
R;
如图(二),连接OB、OC,过O作OE⊥BC于E,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=
R,
故BC=
R;
故圆内接正三角形、正方形、正六边形的边长之比为
R:
R=
:
.
故答案为:
:
.
 解:设圆的半径为R,
解:设圆的半径为R,如图(一),连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB•cos30°=
| ||
| 2 |
故BC=2BD=
| 3 |
如图(二),连接OB、OC,过O作OE⊥BC于E,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=
| ||
| 2 |
故BC=
| 2 |
故圆内接正三角形、正方形、正六边形的边长之比为
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查的是圆内接正三角形、正方形的性质,根据题意画出图形,作出辅助线构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
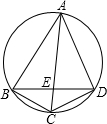 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于