题目内容
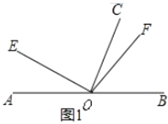
【题目】如图,已知直线![]() 射线
射线![]() ,
,![]() 。
。![]() 是射线
是射线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() 。作
。作![]() ,交直线
,交直线![]() 于点
于点![]() ,
,![]() 平分
平分![]() 。
。

(1)若点![]() 都在点
都在点![]() 的右侧。
的右侧。
①求![]() 的度数;
的度数;
②若![]() ,求
,求![]() 的度数。
的度数。
(2)在点![]() 的运动过程中,是否存在这样的情形,使
的运动过程中,是否存在这样的情形,使![]() ,若存在,求出
,若存在,求出![]() 的度数;若不存在,请说明理由。
的度数;若不存在,请说明理由。
【答案】(1)①40°;②60°;(2)60°或15°.
【解析】
(1)①根据平行线的性质可知![]() ,再结合角平分线的性质可求得
,再结合角平分线的性质可求得![]() ,进而求解即可.
,进而求解即可.
②根据平行线性质可得![]() ,结合已知条件
,结合已知条件![]() 且
且![]() 可求得
可求得![]() ,根据平行线性质进而可求得
,根据平行线性质进而可求得![]() .
.
(2)根据已知条件设![]() ,则
,则![]() ,分①当点
,分①当点![]() 在点
在点![]() 的右侧时②当点
的右侧时②当点![]() 在点
在点![]() 的左侧时两种情况,结合已知条件进行求解即可.
的左侧时两种情况,结合已知条件进行求解即可.
(1)①∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 平分
平分![]() ,
,
∴![]()
![]()

②∵![]()
∴![]() ,
,
![]() ,
,
∴![]()
又∵![]() ,
,
∴![]()
∴![]()
![]()
∵![]()
∴![]()
(2)设![]() ,则
,则![]() ,
,
①当点![]() 在点
在点![]() 的右侧时,
的右侧时,

则![]() ,
,
∵![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]()
②当点![]() 在点
在点![]() 的左侧时,
的左侧时,

则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]()
∴![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目