题目内容
如图,对称轴为直线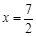 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
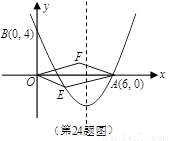
1.求抛物线解析式及顶点坐标;
2.设点E(x,y)是抛物线第四象限上一动点,四边形OEAF是以OA为对角线的平行四边形,求 OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围
OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围
3.若S=24,试判断 OEAF是否为菱形。
OEAF是否为菱形。
4.若点E在⑴中的抛物线上,点F在对称轴上,以O、E、A、F为顶点的四边形能否为平行四边形,若能,求出点E、F的坐标;若不能,请说明理由。(第⑷问不写解答过程,只写结论)
【答案】
1. ;(
;( )
)
2. 因为E在第四象限所以y<0,可得
因为E在第四象限所以y<0,可得 (1<x<6)
(1<x<6)
3.不一定,由S=24可角得x=3或x=4,当时x=3是菱形,当x=4时不是菱形
4.E1 ,F1(
,F1( );E2(
);E2( ),F2(
),F2( );E3(
);E3( ),F3(
),F3( )
)
【解析】略

练习册系列答案
相关题目
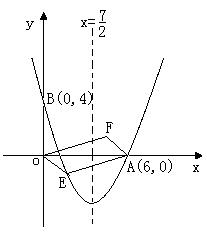
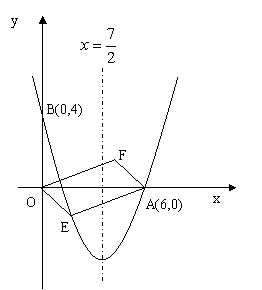 ②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由. 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).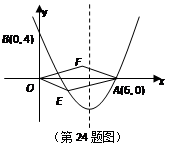
 OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围
OEAF的面积S与x之间的函数关系式,并求出自变量的取值范围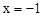 的抛物线
的抛物线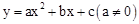 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。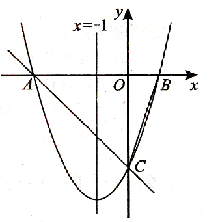
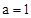 ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。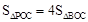 ,求点P的坐标;
,求点P的坐标;