题目内容
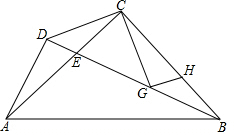 如图,△ABC中,CA=CB,∠ACB=90°,D为△ABC外一点,且AD⊥BD,BD交AC于E,G为BC上一点,且∠BCG=∠DCA,若AD=CG,AB=AC+BH.求证:GH⊥CG.
如图,△ABC中,CA=CB,∠ACB=90°,D为△ABC外一点,且AD⊥BD,BD交AC于E,G为BC上一点,且∠BCG=∠DCA,若AD=CG,AB=AC+BH.求证:GH⊥CG.考点:全等三角形的判定与性质
专题:证明题
分析:延长CG交AB于F,易证△ADC≌△BGC,可得CD=CG,即可求得AC=AF,∠BGF=45°,即可求得BF=BH,即可证明△BGF≌△BGH,可得∠BGH=∠BGF=45°,即可解题.
解答:证明:延长CG交AB于F,
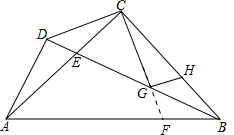
∵∠CBE+∠CEB+∠BCE=180°,∠AED+∠ADE+∠DAE=180°,∠DEA=∠BEC,∠ADE=∠BCE=90°.
∴∠DAE=∠CBE,
在△ADC和△BGC中,
,
∴△ADC≌△BGC(ASA),
∴CD=CG,
∵AD=CG,
∴AD=CD,
∵∠BCG=∠DCA,
∴∠DCG=90°,
∴∠CDG=45°,
∴∠DAC=∠DCA=∠BCG=∠CBG=22.5°,
∴∠ACF=67.5°,
∵AC=BC,
∴∠CAB=∠ABC=45°,
∴∠AFC=67.5°,∠ABG=22.5°,
∴AC=AF,∠BGF=45°,
∵AB=AC+BH,
∴BF=BH,
在△BGF和△BGH中,
,
∴△BGF≌△BGH(SAS),
∴∠BGH=∠BGF=45°,
∴∠CGH=90°,即GH⊥CG.

∵∠CBE+∠CEB+∠BCE=180°,∠AED+∠ADE+∠DAE=180°,∠DEA=∠BEC,∠ADE=∠BCE=90°.
∴∠DAE=∠CBE,
在△ADC和△BGC中,
|
∴△ADC≌△BGC(ASA),
∴CD=CG,
∵AD=CG,
∴AD=CD,
∵∠BCG=∠DCA,
∴∠DCG=90°,
∴∠CDG=45°,
∴∠DAC=∠DCA=∠BCG=∠CBG=22.5°,
∴∠ACF=67.5°,
∵AC=BC,
∴∠CAB=∠ABC=45°,
∴∠AFC=67.5°,∠ABG=22.5°,
∴AC=AF,∠BGF=45°,
∵AB=AC+BH,
∴BF=BH,
在△BGF和△BGH中,
|
∴△BGF≌△BGH(SAS),
∴∠BGH=∠BGF=45°,
∴∠CGH=90°,即GH⊥CG.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ADC≌△BGC和△BGF≌△BGH是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
当甲地高于海平面1500米时,记作“海拔+1500米”,那么乙地低于海平面500米时,记作( )
| A、海拔500米 |
| B、海拔-500米 |
| C、海拔500千米 |
| D、海拔-500千米 |
下列计算中,正确的是( )
| A、3x-x=2x |
| B、6y2-y2=5 |
| C、b4+b3=b7 |
| D、3x+4y=7xy |