题目内容
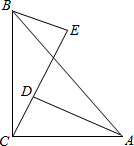 如图∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
如图∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
求证:△ACD≌△CBE.
证明:∵BE⊥CE,AD⊥CE于D,
∴∠CEB=∠ADC=90°,
∵∠BCE+∠ACD=∠ACB=90°,
∠CAD+∠ACD=180°-90°=90°,
∴∠BCE=∠CAD,
在△ACD和△CBE中, ,
,
∴△ACD≌△CBE(AAS).
分析:根据同角的余角相等推出∠BCE=∠CAD,然后利用“角角边”证明即可.
点评:本题考查了全等三角形的判定,比较简单,证明得到∠BCE=∠CAD是解题的关键.
∴∠CEB=∠ADC=90°,
∵∠BCE+∠ACD=∠ACB=90°,
∠CAD+∠ACD=180°-90°=90°,
∴∠BCE=∠CAD,
在△ACD和△CBE中,
 ,
,∴△ACD≌△CBE(AAS).
分析:根据同角的余角相等推出∠BCE=∠CAD,然后利用“角角边”证明即可.
点评:本题考查了全等三角形的判定,比较简单,证明得到∠BCE=∠CAD是解题的关键.

练习册系列答案
相关题目
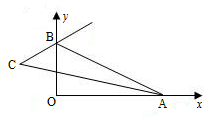 14、如图∠XOY=90°,点A,B分别在射线OX,OY上移动,∠OAB的内角平分线与∠OBA的外角平分线交于点C,试问∠ACB的大小是否变动?为什么?
14、如图∠XOY=90°,点A,B分别在射线OX,OY上移动,∠OAB的内角平分线与∠OBA的外角平分线交于点C,试问∠ACB的大小是否变动?为什么?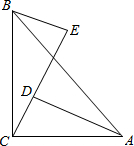 如图∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
如图∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,